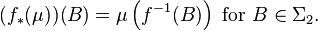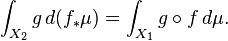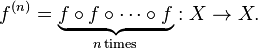Pushforward measure
In measure theory, a pushforward measure (also push forward, push-forward or image measure) is obtained by transferring ("pushing forward") a measure from one measurable space to another using a measurable function.
Definition
Given measurable spaces (X1, Σ1) and (X2, Σ2), a measurable mapping f : X1 → X2 and a measure μ : Σ1 → [0, +∞], the pushforward of μ is defined to be the measure f∗(μ) : Σ2 → [0, +∞] given by
This definition applies mutatis mutandis for a signed or complex measure.
Main property: Change of variables formula
Theorem:[1] A measurable function g on X2 is integrable with respect to the pushforward measure f∗(μ) if and only if the composition  is integrable with respect to the measure μ. In that case, the integrals coincide, i.e.,
is integrable with respect to the measure μ. In that case, the integrals coincide, i.e.,
Examples and applications
- A natural "Lebesgue measure" on the unit circle S1 (here thought of as a subset of the complex plane C) may be defined using a push-forward construction and Lebesgue measure λ on the real line R. Let λ also denote the restriction of Lebesgue measure to the interval [0, 2π) and let f : [0, 2π) → S1 be the natural bijection defined by f(t) = exp(i t). The natural "Lebesgue measure" on S1 is then the push-forward measure f∗(λ). The measure f∗(λ) might also be called "arc length measure" or "angle measure", since the f∗(λ)-measure of an arc in S1 is precisely its arc length (or, equivalently, the angle that it subtends at the centre of the circle.)
- The previous example extends nicely to give a natural "Lebesgue measure" on the n-dimensional torus Tn. The previous example is a special case, since S1 = T1. This Lebesgue measure on Tn is, up to normalization, the Haar measure for the compact, connected Lie group Tn.
- Gaussian measures on infinite-dimensional vector spaces are defined using the push-forward and the standard Gaussian measure on the real line: a Borel measure γ on a separable Banach space X is called Gaussian if the push-forward of γ by any non-zero linear functional in the continuous dual space to X is a Gaussian measure on R.
- Consider a measurable function f : X → X and the composition of f with itself n times:
- This iterated function forms a dynamical system. It is often of interest in the study of such systems to find a measure μ on X that the map f leaves unchanged, a so-called invariant measure, one for which f∗(μ) = μ.
- One can also consider quasi-invariant measures for such a dynamical system: a measure μ on X is called quasi-invariant under f if the push-forward of μ by f is merely equivalent to the original measure μ, not necessarily equal to it.
A generalization
In general, any measurable function can be pushed forward, the push-forward then becomes a linear operator, known as the transfer operator or Frobenius–Perron operator. This operator typically satisfies the requirements of the Frobenius–Perron theorem, and the maximal eigenvalue of this theorem corresponds to the invariant measure. The adjoint to the push-forward is the pullback; as an operator on spaces of functions on measurable spaces, it is the composition operator or Koopman operator.
Notes
References
- Bogachev, Vladimir I. (2007), Measure Theory, Berlin: Springer Verlag, ISBN 9783540345138
- Teschl, Gerald (2015), Topics in Real and Functional Analysis