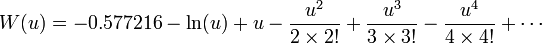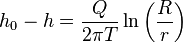Aquifer test
An aquifer test (or a pumping test) is conducted to evaluate an aquifer by "stimulating" the aquifer through constant pumping, and observing the aquifer's "response" (drawdown) in observation wells. Aquifer testing is a common tool that hydrogeologists use to characterize a system of aquifers, aquitards and flow system boundaries.
A slug test is a variation on the typical aquifer test where an instantaneous change (increase or decrease) is made, and the effects are observed in the same well. This is often used in geotechnical or engineering settings to get a quick estimate (minutes instead of days) of the aquifer properties immediately around the well.
Aquifer tests are typically interpreted by using an analytical model of aquifer flow (the most fundamental being the Theis solution) to match the data observed in the real world, then assuming that the parameters from the idealized model apply to the real-world aquifer. In more complex cases, a numerical model may be used to analyze the results of an aquifer test, but adding complexity does not ensure better results (see parsimony).
Aquifer testing differs from well testing in that the behaviour of the well is primarily of concern in the latter, while the characteristics of the aquifer are quantified in the former. Aquifer testing also often utilizes one or more monitoring wells, or piezometers ("point" observation wells). A monitoring well is simply a well which is not being pumped (but is used to monitor the hydraulic head in the aquifer). Typically monitoring and pumping wells are screened across the same aquifers.
General characteristics
Most commonly an aquifer test is conducted by pumping water from one well at a steady rate and for at least one day, while carefully measuring the water levels in the monitoring wells. When water is pumped from the pumping well the pressure in the aquifer that feeds that well declines. This decline in pressure will show up as drawdown (change in hydraulic head) in an observation well. Drawdown decreases with radial distance from the pumping well and drawdown increases with the length of time that the pumping continues.
The aquifer characteristics which are evaluated by most aquifer tests are:
- Hydraulic conductivity The rate of flow of water through a unit cross sectional area of an aquifer, at a unit hydraulic gradient. In US units the rate of flow is in gallons per day per square foot of cross sectional area; in SI units hydraulic conductivity is usually quoted in m3 per day per m2. Units are frequently shortened to metres per day or equivalent.
- Specific storage or storativity: a measure of the amount of water a confined aquifer will give up for a certain change in head;
- Transmissivity The rate at which water is transmitted through whole thickness and unit width of an aquifer under a unit hydraulic gradient. It is equal to the hydraulic conductivity times the thickness of an aquifer;
Additional aquifer characteristics which are sometimes evaluated, depending on the type of aquifer, include:
- Specific yield or drainable porosity: a measure of the amount of water an unconfined aquifer will give up when completely drained;
- Leakage coefficient: some aquifers are bounded by aquitards which slowly give up water to the aquifer, providing additional water to reduce drawdown;
- The presence of aquifer boundaries (recharge or no-flow) and their distance from the pumped well and piezometers.
Analysis methods
An appropriate model or solution to the groundwater flow equation must be chosen to fit to the observed data. There are many different choices of models, depending on what factors are deemed important including:
- leaky aquitards,
- unconfined flow (delayed yield),
- partial penetration of the pumping and monitoring wells,
- finite wellbore radius — which can lead to wellbore storage,
- dual porosity (typically in fractured rock),
- anisotropic aquifers,
- heterogeneous aquifers,
- finite aquifers (the effects of physical boundaries are seen in the test), and
- combinations of the above situations.
Nearly all aquifer test solution methods are based on the Theis solution; it is built upon the most simplifying assumptions. Other methods relax one or more of the assumptions the Theis solution is built on, and therefore they get a more flexible (and more complex) result.
Transient Theis solution
The Theis equation was created by Charles Vernon Theis (working for the US Geological Survey) in 1935,[1] from heat transfer literature (with the mathematical help of C.I. Lubin), for two-dimensional radial flow to a point source in an infinite, homogeneous aquifer. It is simply
where s is the drawdown (change in hydraulic head at a point since the beginning of the test), u is a dimensionless time parameter, Q is the discharge (pumping) rate of the well (volume divided by time, or m³/s), T and S are the transmissivity and storativity of the aquifer around the well (m²/s and unitless, respectively), r is the distance from the pumping well to the point where the drawdown was observed (m), t is the time since pumping began (seconds), and W(u) is the "Well function" (called the exponential integral, E1, in non-hydrogeology literature). The well function is approximated by the infinite series
Typically this equation is used to find the average T and S values near a pumping well, from drawdown data collected during an aquifer test. This is a simple form of inverse modeling, since the result (s) is measured in the well, r, t, and Q are observed, and values of T and S which best reproduce the measured data are put into the equation until a best fit between the observed data and the analytic solution is found.
The Theis solution is based on the following assumptions:
- The flow in the aquifer is adequately described by Darcy's law (i.e. Re<10).
- homogeneous, isotropic, confined aquifer,
- well is fully penetrating (open to the entire thickness (b) of aquifer),
- the well has zero radius (it is approximated as a vertical line) — therefore no water can be stored in the well,
- the well has a constant pumping rate Q,
- the head loss over the well screen is negligible,
- aquifer is infinite in radial extent,
- horizontal (not sloping), flat, impermeable (non-leaky) top and bottom boundaries of aquifer,
- groundwater flow is horizontal
- no other wells or long term changes in regional water levels (all changes in potentiometric surface are the result of the pumping well alone)
Even though these assumptions are rarely all met, depending on the degree to which they are violated (e.g., if the boundaries of the aquifer are well beyond the part of the aquifer which will be tested by the pumping test) the solution may still be useful.
Steady-state Thiem solution
Steady-state radial flow to a pumping well is commonly called the Thiem solution,[2] it comes about from application of Darcy's law to cylindrical shell control volumes (i.e., a cylinder with a larger radius which has a smaller radius cylinder cut out of it) about the pumping well; it is commonly written as:
In this expression h0 is the background hydraulic head, h0-h is the drawdown at the radial distance r from the pumping well, Q is the discharge rate of the pumping well (at the origin), T is the transmissivity, and R is the radius of influence, or the distance at which the head is still h0. These conditions (steady-state flow to a pumping well with no nearby boundaries) never truly occur in nature, but it can often be used as an approximation to actual conditions; the solution is derived by assuming there is a circular constant head boundary (e.g., a lake or river in full contact with the aquifer) surrounding the pumping well at a distance R.
Sources of error
Of critical importance in both aquifer and well testing is the accurate recording of data. Not only must water levels and the time of the measurement be carefully recorded, but the pumping rates must be periodically checked and recorded. An unrecorded change in pumping rate of as little as 2% can be misleading when the data are analysed.
References
- ↑ Theis, Charles V. (1935). "The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using ground-water storage". Transactions, American Geophysical Union 16: 519–524.
- ↑ Thiem, Günther (1906). "Hydrologische methoden" (in German). Leipzig: J. M. Gebhardt: 56
Additional reading
The US Geological Survey has some very useful free references on pumping test interpretation:
- Ferris, J.G.; Knowles, D.B.; Brown, R.H.; Stallman, R.W. (1962). Theory of Aquifer Tests (PDF). Water Supply Paper 1536-E. U.S. Geological Survey.
- Stallman, R.W. (1971). "Chapter B1". Aquifer-Test Design, Observation, and Data Analysis (PDF). Book 3, Applications of Hydraulics. U.S. Geological Survey.
- Reed, J.E. (1980). "Chapter B3". Type Curves for Selected Problems of Flow to Wells in Confined Aquifers (PDF). Book 3, Applications of Hydraulics. U.S. Geological Survey.
- Franke, 0.L.; Reilly, T.E.; Bennett, G.D. (1987). "Chapter B5". Definition of Boundary and Initial Conditions in the Analysis of Saturated Ground-Water Flow Systems — An Introduction (PDF). Book 3, Applications of Hydraulics. U.S. Geological Survey.
Some commercial printed references on aquifer test interpretation:
- Batu, V. (1998). Aquifer Hydraulics: a comprehensive guide to hydrogeologic data analysis. Wiley-Interscience. ISBN 0-471-18502-7.
- Good summary of the most popular aquifer test methods, good for practicing hydrogeologists
- Dawson, K.J.; Istok, J.D. (1991). Aquifer Testing: design and analysis of pumping and slug tests. Lewis Publishers. ISBN 0-87371-501-2.
- Thorough, a bit more mathematical than Batu
- Kruseman, G.P.; de Ridder, N.A. (1990). Analysis and Evaluation of Pumping Test Data (PDF) (Second ed.). Wageningen, The Netherlands: International Institute for Land Reclamation and Improvement. ISBN 90-70754-20-7.
- Excellent treatment of most aquifer test analysis methods (but it is a hard-to-find book).
- Boonstra, J.; Kselik, R.A.L. (2002). SATEM 2002: Software for aquifer test evaluation. Wageningen, The Netherlands: International Institute for Land Reclamation and Improvement. ISBN 90-70754-54-1.
- Sindalovskiy, L.N. (2011). ANSDIMAT - software for aquifer parameters estimation. St. Petersburg, Russia (in Russian): Nauka. ISBN 978-5-02-025477-0.
More book titles can be found in the further reading section of the hydrogeology article, most of which contain some material on aquifer test analysis or the theory behind these test methods.
Analysis software
- Water Resources Applications Software from the US Geological Survey
- Schlumberger Water Services – Pumping test and slug test data analysis software
- ANSDIMAT – advanced commercial software
- AQTESOLV – standard commercial software
- MLU for Windows LT – Free software for pumping test and slug test analysis in one or two aquifer systems
- VINMOD Multi-Well – Groundwater pollution analysis using pumping tests and pollution parameters from pumped groundwater
- Online Theis Equation Calculator - Free online calculator solves Theis equation and displays results graphically
- Hytool - Open source toolbox for pumping and build up tests interpretation on Matlab
See also
| ||||||
![\begin{align}
s &= \frac{Q}{4\pi T}W(u) \\[0.5em]
u &= \frac{r^2 S}{4Tt}
\end{align}](../I/m/0b12f51858dd1524a2a4a3f0503c8a71.png)