Pulsatile flow
In fluid dynamics, a flow with periodic variations is known as pulsatile flow. The cardiovascular system of chordate animals is a very good example where pulsatile flow is found. Pulsatile flow is also observed in engines and hydraulic systems as a result of rotating mechanisms belonging to them.
Derivation
To obtain the velocity profile of non-stationary flow, one must solve the equations of motion and continuity. Depending on the complexity of the boundary conditions, the problem's analytic solution may be impracticable and thus numerical simulations would be necessary. An analytical solution is here given assuming the following hypothesis:
- Fluid is homogeneous, incompressible and Newtonian;
- Tube wall is rigid, circular and cylindrical;
- Motion is laminar, axisymmetric and parallel to the tube's axis;
- Boundary conditions are axisymmetry at the centre and no-slip condition on the wall;
- Pressure gradient drives the fluid;
- Gravitation has no effect on the fluid. [1][2]
The field equations Navier-Stokes equation and the equation of continuity are simplified as
and
The pressure gradient is a general periodic function
Flow velocity profile is driven by the pressure, resulting in
Substituting the pressure gradient and flow velocity profile in the Navier-Stokes equation gives us
With the boundary conditions satisfied, the general solution is
where 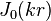 is the Bessel function of first kind and order zero,
is the Bessel function of first kind and order zero, 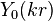 is the Bessel function of second kind and order zero, being
is the Bessel function of second kind and order zero, being  a constant.
a constant.  and
and 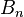 are arbitrary constants and
are arbitrary constants and  is the dimensionless Womersley number. In order to determine
is the dimensionless Womersley number. In order to determine  and
and 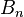 the axisymetic boundary condition is used, i.e.
the axisymetic boundary condition is used, i.e. 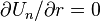 , then the derivatives
, then the derivatives 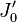 and
and 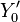 approaches infinity. Hence
approaches infinity. Hence 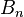 must vanish. And the boundary condition at the wall gives us
must vanish. And the boundary condition at the wall gives us
Solving this equation for  , we obtain the amplitudes of the velocity profile
, we obtain the amplitudes of the velocity profile
which leads to the velocity profile itself
The velocity profile depends on Womersley number  .
.
Cardiovascular flow
These pulsating characteristics have been shown to be a result of two pumps. As the primary pump, the heart causes the blood flow and velocity to oscillate from zero to very high rates as the valves at the entrances and exits to the ventricles intermittently close and open with each beat of the heart. The second pump is a result of the respiratory and skeletal systems, which exert their greatest action on venous flow.[3] Specifically pulsation that result from the release of blood from the left ventricle show that they exhibit non-linear, transient pulsations in pressure and flow. These create complex pulse patterns which are further propagated through the rest of the network. This results in variations in the applied shear stress to the layer of endothelial cells covering the vessel wall. Depending upon the amount of stress, the endothelial cells will react releasing chemicals that either induce dilation or constriction of the smooth muscle surrounding the vessel.
It is nearly impossible to mathematically model such a flow using the standard Navier-Stokes equations. Rather than give an equation that can model the flow, which has proven to be near impossible; the Womersley number is used. This dimensionless number has been developed to give a measure of the frequency and magnitude of pulsations rather than a model of the actual flow.
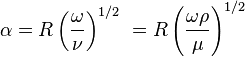
As you can see, the equation can take on two forms by substituting mu/rho for nu. It can also be shown that Womersley number is primarily influenced by the size of the vessel which can be shown in the table below. Since the density of blood and blood viscosity remain fairly constant (with slight variations throughout) the value of the square root will be similar for all, thus vessel size is most important.
| Section | Radius (cm) | alpha |
|---|---|---|
| Ascending Aorta | 0.75 | 14.628 |
| Descending Aorta | 0.65 | 12.677 |
| Abdominal Aorta | 0.45 | 8.777 |
| Femoral Artery | 0.2 | 3.901 |
| Cartoid Artery | 0.25 | 4.876 |
| Arteriole | 0.0025 | 0.049 |
| Capillary | 0.0003 | 0.006 |
| Venule | 0.002 | 0.039 |
| Inferior Vena Cava | 0.5 | 9.752 |
| Main Pulmonary artery | 0.85 | 16.578 |
These values were calculated using a cardiac frequency of 2 Hz, a blood density of 1060 kg/m^3 at 37 C, and a dynamic viscosity of 0.0035 Pa-s
References
- ↑ Fung, Y. C. (1990). Biomechanics – Motion, flow, stress and growth. New York (USA): Springer-Verlag. p. 569.
- ↑ Nield, D.A.; Kuznetsov, A.V. (2007). "Forced convection with laminar pulsating flow in a channel or tube". International Journal of Thermal Sciences 46 (6): 551–560. doi:10.1016/j.ijthermalsci.2006.07.011.
- ↑ Lee, B. Y., and Trainor, F. S. (1973). Peripheral Vascular Surgery: Hemodynamics of Arterial Pulsatile Blood Flow. New York: Appleton-Century-Crofts. p. 270.
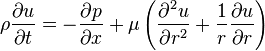
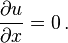
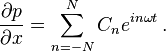
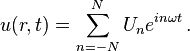
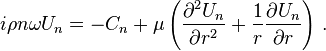
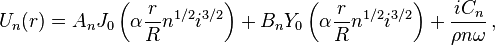
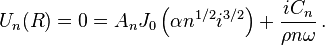
![U_n(r) = \frac{iC_n}{\rho n \omega} \left[ 1 - \frac{J_0(\alpha \frac{r}{R} n^{1/2}i^{3/2})}{J_0(\alpha n^{1/2}i^{3/2})} \right] \, ,](../I/m/b22cbb6b270401ee1c418af5989ba4f7.png)
![u(r) = \sum^N_{n=-N} \frac{iC_n}{\rho n \omega} \left[ 1 - \frac{J_0(\alpha \frac{r}{R} n^{1/2}i^{3/2})}{J_0(\alpha n^{1/2}i^{3/2})} \right] e^{in\omega t} \, .](../I/m/451baf55beccbaa72be37e91a5472387.png)