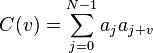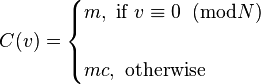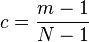Pseudorandom binary sequence

A pseudorandom binary sequence (PRBS) is a binary sequence that, while generated with a deterministic algorithm, is difficult to predict^[1] and exhibits statistical behavior similar to a truly-random sequence. PRBS are used in telecommunication, encryption, simulation, correlation technique and time-of-flight spectroscopy.

Details

A binary sequence (BS) is a sequence 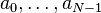$a_0,\ldots, a_{N-1}$ of $N$ bits, i.e.

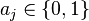a_j\in \{0,1\}

for

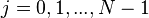j=0,1,...,N-1

A BS consists of 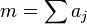$m=\sum a_j$ ones and $N-m$ zeros.

A BS is a pseudorandom binary sequence (PRBS) if^[2] its autocorrelation function, given by

C(v)=\sum_{j=0}^{N-1} a_ja_{j+v}

has only two values:

C(v)= \begin{cases} m, \mbox{ if } v\equiv 0\;\; (\mbox{mod}N)\\ \\ mc, \mbox{ otherwise } \end{cases}

where

c=\frac{m-1}{N-1}

is called the duty cycle of the PRBS, similar to the duty cycle of a continuous time signal. For a maximum length sequence, where 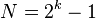$N = 2^k - 1$ , the duty cycle is 1/2.

A PRBS is 'pseudorandom', because, although it is in fact deterministic, it seems to be random in a sense that the value of an $a_j$ element is independent of the values of any of the other elements, similar to real random sequences.

A PRBS can be stretched to infinity by repeating it after $N$ elements, but it will then be cyclical and thus non-random. In contrast, truly random sequence sources, such as sequences generated by radioactive decay or by white noise, are infinite (no pre-determined end or cycle-period). However, as a result of this predictability, PRBS signals can be used as reproducible patterns (for example, signals used in testing telecommunications signal paths).^[3]

Practical implementation

Pseudorandom binary sequences can be generated using linear feedback shift registers.^[4]

Some common^[5]^[6]^[7]^[8] sequence generating polynomials are

PRBS7 =

x^{7} + x^{6} + 1

PRBS15 =

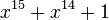
x^{15} + x^{14} + 1

PRBS23 =

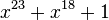
x^{23} + x^{18} + 1

PRBS31 =

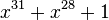
x^{31} + x^{28} + 1

An example of generating a "PRBS-7" sequence can be expressed in C as

#include <stdio.h>
#include <stdint.h>
#include <stdlib.h>
    
int main(int argc, char* argv[]) {
    uint8_t start = 0x02;
    uint8_t a = start;
    int i;    
    for(i = 1;; i++) {
        int newbit = (((a >> 6) ^ (a >> 5)) & 1);
        a = ((a << 1) | newbit) & 0x7f;
        printf("%x\n", a);
        if (a == start) {
            printf("repetition period is %d\n", i);
            break;
        }
    }
}

In this particular case, "PRBS-7" has a repetition period of 127 bits.

Notation

The PRBSk or PRBS-k notation (such as "PRBS7" or "PRBS-7") gives an indication of the size of the sequence. 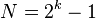$N = 2^k - 1$ is the maximum number^[3]^:§3 of bits that be in the sequence. The k indicates the size of a unique word of data in the sequence. If you segment the N bits of data into every possible word of length k, you will be able to list every possible combination of 0s and 1s for a k-bit binary word, with the exception of the all-0s word.^[3]^:§2 For example, PRBS3 = "1011100" could be generated from 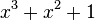$x^{3} + x^{2} + 1$ .^[5] If you take every sequential group of three bit words in the PRBS3 sequence (wrapping around to the beginning for the last few three-bit words), you will find the following 7 words:

  "1011100" → 101
  "1011100" → 011
  "1011100" → 111
  "1011100" → 110
  "1011100" → 100
  "1011100" → 001 (requires wrap)
  "1011100" → 010 (requires wrap)

Those 7 words are all of the 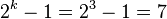$2^k - 1 = 2^3 - 1 = 7$ possible non-zero 3-bit binary words, not in numeric order. The same holds true for any PRBSk, not just PRBS3.^[3]^:§2

References

↑ "PRBS Pseudo Random Bit Sequence Generation". TTi. Retrieved 21 January 2016.
↑ Naszodi, Laszlo. "Articles on Correlation and Calibration". Archived from the original on 11 November 2013.
1 2 3 4 "ITU-T Recommendation O.150". October 1992.
↑ Paul H. Bardell, William H. McAnney, and Jacob Savir, "Built-In Test for VLSI: Pseudorandom Techniques", John Wiley & Sons, New York, 1987.
1 2 Tomlinson, Kurt (4 February 2015). "PRBS (Pseudo-Random Binary Sequence)". Bloopist. Retrieved 21 January 2016.
↑ Koopman, Philip. "Maximal Length LFSR Feedback Terms". Retrieved 21 January 2016.
↑ "What are the PRBS7, PRBS15, PRBS23, and PRBS31 polynomials used in the Altera Transceiver Toolkit?". Altera. 14 February 2013. Retrieved 21 January 2016.
↑ Riccardi, Daniele; Novellini, Paolo (10 January 2011). "An Attribute-Programmable PRBS Generator and Checker (XAP884)" (PDF). Xilinx. Table 3:Configuration for PRBS Polynomials Most Used to Test Serial Lines. Retrieved 21 January 2016.

External links

A011686 lists the bit sequence for PRBS7 = $x^{7} + x^{6} + 1$

This article is issued from Wikipedia - version of the Friday, January 22, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.