Pseudocompact space
In mathematics, in the field of topology, a topological space is said to be pseudocompact if its image under any continuous function to R is bounded. Many authors include the request that the space is completely regular right in the definition of pseudocomapctness. Pseudocompact spaces were defined by Edwin Hewitt in 1948.[1]
Properties related to pseudocompactness
- For a Tychonoff space X to be pseudocompact requires that every locally finite collection of non-empty open sets of X be finite. There are many equivalent conditions for pseudocompactness (sometimes some separation axiom should be assumed); a large number of them are quoted in Stephenson 2003. Some historical remarks about earlier results can be found in Engelking 1989, p. 211.
- Every countably compact space is pseudocompact. For normal Hausdorff spaces the converse is true.
- As a consequence of the above result, every sequentially compact space is pseudocompact. The converse is true for metric spaces. As sequential compactness is an equivalent condition to compactness for metric spaces this implies that compactness is an equivalent condition to pseudocompactness for metric spaces also.
- The weaker result that every compact space is pseudocompact is easily proved: the image of a compact space under any continuous function is compact, and every compact set in a metric space is bounded.
- If Y is the continuous image of pseudocompact X, then Y is pseudocompact. Note that for continuous functions g : X → Y and h : Y → R, the composition of g and h, called f, is a continuous function from X to the real numbers. Therefore, f is bounded, and Y is pseudocompact.
- Let X be an infinite set given the particular point topology. Then X is neither compact, sequentially compact, countably compact, paracompact nor metacompact. However, since X is hyperconnected, it is pseudocompact. This shows that pseudocompactness doesn't imply any other (known) form of compactness.
- For a Hausdorff space X to be compact requires that X be pseudocompact and realcompact (see Engelking 1968, p. 153).
- For a Tychonoff space X to be compact requires that X be pseudocompact and metacompact (see Watson).
Pseudocompact topological groups
A relatively refined theory is available for pseudocompact topological groups.[2] In particular, W. W. Comfort and Kenneth A. Ross proved that a product of pseudocompact topological groups is still pseudocompact (this might fail for arbitrary topological spaces).[3]
Notes
- ↑ Rings of real-valued continuous functions, I, Trans. Amer. Math. Soc. 64 (1948), 45-99.
- ↑ See, for example, Mikhail Tkachenko, Topological Groups: Between Compactness and
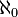 -boundedness, in Mirek Husek and Jan van Mill (eds.), Recent Progress in General Topology II, 2002 Elsevier Science B.V.
-boundedness, in Mirek Husek and Jan van Mill (eds.), Recent Progress in General Topology II, 2002 Elsevier Science B.V. - ↑ Comfort, W. W. and Ross, K. A., Pseudocompactness and uniform contmuity in topological groups, Pacific J. Math. 16, 483-496, 1966.
See also
References
- Engelking, Ryszard (1968), Outline of General Topology, translated from Polish, Amsterdam: North-Holland.
- Engelking, Ryszard (1989), General Topology, Berlin: Heldermann Verlag.
- Kerstan, Johannes (1957), "Zur Charakterisierung der pseudokompakten Räume", Mathematische Nachrichten 16 (5–6): 289–293, doi:10.1002/mana.19570160505.
- Stephenson, R.M. Jr (2003), Pseudocompact Spaces, Chapter d-7 in Encyclopedia of General Topology, Edited by: Klaas Pieter Hart, Jun-iti Nagata and Jerry E. Vaughan, Pages 177-181, Amsterdam: Elsevier B. V..
- Watson, W. Stephen (1981), "Pseudocompact metacompact spaces are compact", Proc. Amer. Math. Soc. 81: 151–152, doi:10.1090/s0002-9939-1981-0589159-1.
- Willard, Stephen (1970), General Topology, Reading, Mass.: Addison-Wesley.
- Yan-Min, Wang (1988), "New characterisations of pseudocompact spaces", Bull. Austral. Math. Soc. 38 (2): 293–298, doi:10.1017/S0004972700027568.
External links
- M.I. Voitsekhovskii (2001), "Pseudo-compact space", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4.
- Pseudocompact space at PlanetMath.org. .
This article is issued from Wikipedia - version of the Saturday, January 30, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.