Generalized inverse
In mathematics, a generalized inverse of a matrix A is a matrix that has some properties of the inverse matrix of A but not necessarily all of them. Formally, given a matrix  and a matrix
and a matrix  ,
, 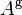 is a generalized inverse of
is a generalized inverse of  if it satisfies the condition
if it satisfies the condition  .
.
The purpose of constructing a generalized inverse is to obtain a matrix that can serve as the inverse in some sense for a wider class of matrices than invertible ones. A generalized inverse exists for an arbitrary matrix, and when a matrix has an inverse, then this inverse is its unique generalized inverse. Some generalized inverses can be defined in any mathematical structure that involves associative multiplication, that is, in a semigroup.
Types of generalized inverses
The Penrose conditions are used to define different generalized inverses: for  and
and 
| 1.) |  |
| 2.) |  |
| 3.) |  |
| 4.) | 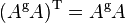 . . |
If 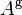 satisfies condition (1.), it is a generalized inverse of
satisfies condition (1.), it is a generalized inverse of  , if it satisfies conditions (1.) and (2.) then it is a generalized reflexive inverse of
, if it satisfies conditions (1.) and (2.) then it is a generalized reflexive inverse of  , and if it satisfies all 4 conditions, then it is a Moore–Penrose pseudoinverse of
, and if it satisfies all 4 conditions, then it is a Moore–Penrose pseudoinverse of  .
.
Other various kinds of generalized inverses include
- One-sided inverse (left inverse or right inverse) If the matrix A has dimensions
 and is full rank then use the left inverse if
and is full rank then use the left inverse if  and the right inverse if
and the right inverse if 
- Left inverse is given by
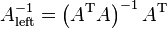 , i.e.
, i.e.  where
where 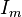 is the
is the  identity matrix.
identity matrix. - Right inverse is given by
 , i.e.
, i.e.  where
where  is the
is the  identity matrix.
identity matrix.
- Left inverse is given by
- Drazin inverse
- Bott–Duffin inverse
- Moore–Penrose pseudoinverse
Uses
Any generalized inverse can be used to determine if a system of linear equations has any solutions, and if so to give all of them.[1] If any solutions exist for the n × m linear system
with vector  of unknowns and vector b of constants, all solutions are given by
of unknowns and vector b of constants, all solutions are given by
parametric on the arbitrary vector w, where 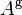 is any generalized inverse of
is any generalized inverse of  Solutions exist if and only if
Solutions exist if and only if  is a solution – that is, if and only if
is a solution – that is, if and only if 
See also
References
- ↑ James, M. (June 1978). "The generalised inverse". Mathematical Gazette 62: 109–114. doi:10.2307/3617665.
- Yoshihiko Nakamura (1991). * Advanced Robotics: Redundancy and Optimization. Addison-Wesley. ISBN 0201151987.
- Zheng, B; Bapat, R. B. (2004). "Generalized inverse A(2)T,S and a rank equation". Applied Mathematics and Computation 155: 407–415. doi:10.1016/S0096-3003(03)00786-0.
- S. L. Campbell and C. D. Meyer (1991). Generalized Inverses of Linear Transformations. Dover. ISBN 978-0-486-66693-8.
- Adi Ben-Israel and Thomas N.E. Greville (2003). Generalized inverses. Theory and applications (2nd ed.). New York, NY: Springer. ISBN 0-387-00293-6.
- C. R. Rao and C. Radhakrishna Rao and Sujit Kumar Mitra (1971). Generalized Inverse of Matrices and its Applications. New York: John Wiley & Sons. p. 240. ISBN 0-471-70821-6.
External links
- 15A09 Matrix inversion, generalized inverses in Mathematics Subject Classification, MathSciNet search

![x=A^{\mathrm g}b + [I-A^{\mathrm g}A]w](../I/m/b007c0ee7531785cb8dc973a71c0bb9e.png)