Pseudo algebraically closed field

In mathematics, a field $K$ is pseudo algebraically closed if it satisfies certain properties which hold for any algebraically closed field. The concept was introduced by James Ax in 1967.^[1]

Formulation

A field K is pseudo algebraically closed (usually abbreviated by PAC^[2]) if one of the following equivalent conditions holds:

Each absolutely irreducible variety $V$ defined over $K$ has a $K$ -rational point.
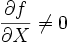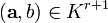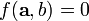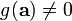For each absolutely irreducible polynomial $f\in K[T_1,T_2,\cdots ,T_r,X]$ with $\frac{\partial f}{\partial X}\not =0$ and for each nonzero $g\in K[T_1,T_2,\cdots ,T_r]$ there exists $(\textbf{a},b)\in K^{r+1}$ such that $f(\textbf{a},b)=0$ and $g(\textbf{a})\not =0$ .
Each absolutely irreducible polynomial $f\in K[T,X]$ has infinitely many $K$ -rational points.
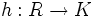If $R$ is a finitely generated integral domain over $K$ with quotient field which is regular over $K$ , then there exist a homomorphism $h:R\to K$ such that 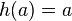$h(a)=a$ for each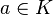 $a\in K$

Examples

Algebraically closed fields and separably closed fields are always PAC.

Pseudo-finite fields and hyper-finite fields are PAC.

A non-principal ultraproduct of distinct finite fields is (pseudo-finite and hence^[3]) PAC.^[2] Ax deduces this from the Riemann hypothesis for curves over finite fields.^[1]

Infinite algebraic extensions of finite fields are PAC.^[4]

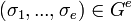The PAC Nullstellensatz. The absolute Galois group $G$ of a field $K$ is profinite, hence compact, and hence equipped with a normalized Haar measure. Let $K$ be a countable Hilbertian field and let $e$ be a positive integer. Then for almost all $e$ -tuple $(\sigma_1,...,\sigma_e)\in G^e$ , the fixed field of the subgroup generated by the automorphisms is PAC. Here the phrase "almost all" means "all but a set of measure zero".^[5] (This result is a consequence of Hilbert's irreducibility theorem.)

Let K be the maximal totally real Galois extension of the rational numbers and i the square root of -1. Then K(i) is PAC.

Properties

The Brauer group of a PAC field is trivial,^[6] as any Severi–Brauer variety has a rational point.^[7]
The absolute Galois group of a PAC field is a projective profinite group; equivalently, it has cohomological dimension at most 1.^[7]
A PAC field of characteristic zero is C1.^[8]

References

1 2 Fried & Jarden (2008) p.218
1 2 Fried & Jarden (2008) p.192
↑ Fried & Jarden (2008) p.449
↑ Fried & Jarden (2008) p.196
↑ Fried & Jarden (2008) p.380
↑ Fried & Jarden (2008) p.209
1 2 Fried & Jarden (2008) p.210
↑ Fried & Jarden (2008) p.462

Fried, Michael D.; Jarden, Moshe (2008). Field arithmetic. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge 11 (3rd revised ed.). Springer-Verlag. ISBN 978-3-540-77269-9. Zbl 1145.12001. CS1 maint: Extra text (link)

This article is issued from Wikipedia - version of the Friday, December 13, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.