Pseudo-determinant

In linear algebra and statistics, the pseudo-determinant^[1] is the product of all non-zero eigenvalues of a square matrix. It coincides with the regular determinant when the matrix is non-singular.

Definition

The pseudo-determinant of a square n-by-n matrix A may be defined as:

|\mathbf{A}|_+ = \lim_{\alpha\to 0} \frac{|\mathbf{A} + \alpha \mathbf{I}|}{\alpha^{n-\operatorname{rank}(\mathbf{A})}}

where |A| denotes the usual determinant, I denotes the identity matrix and rank(A) denotes the rank of A.

Definition of pseudo determinant using Vahlen Matrix

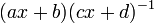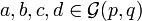The Vahlen matrix of a conformal transformation, the Möbius transformation (i.e. $(ax+b)(cx+d)^{-1}$ for $a,b,c,d\in \mathcal {G}(p,q)$ )) is defined as $[f]=::\begin{bmatrix}a & b \\c & d \end{bmatrix}$ . By the pseudo determinant of the Vahlen matrix for the conformal transformation, we mean

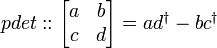
$pdet:: \begin{bmatrix}a & b\\ c& d\end{bmatrix} =ad^\dagger -bc^\dagger$

If $pdet[f]>0$ , the transformation is sense-preserving (rotation) whereas if the $pdet[f]<0$ , the transformation is sense-preserving (reflection).

Computation for positive semi-definite case

If $A$ is positive semi-definite, then the singular values and eigenvalues of $A$ coincide. In this case, if the singular value decomposition (SVD) is available, then $|\mathbf {A}|_+$ may be computed as the product of the non-zero singular values. If all singular values are zero, then the pseudo-determinant is 1.

Application in statistics

If a statistical procedure ordinarily compares distributions in terms of the determinants of variance-covariance matrices then, in the case of singular matrices, this comparison can be undertaken by using a combination of the ranks of the matrices and their pseudo-determinants, with the matrix of higher rank being counted as "largest" and the pseudo-determinants only being used if the ranks are equal.^[2] Thus pseudo-determinants are sometime presented in the outputs of statistical programs in cases where covariance matrices are singular.^[3]

References

↑ Minka, T.P. (2001). "Inferring a Gaussian Distribution". PDF
↑ SAS documentation on "Robust Distance"
↑ Bohling, Geoffrey C. (1997) "GSLIB-style programs for discriminant analysis and regionalized classification", Computers & Geosciences, 23 (7), 739–761 doi: 10.1016/S0098-3004(97)00050-2

This article is issued from Wikipedia - version of the Wednesday, November 26, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.