Pseudo-deltoidal icositetrahedron
| Pseudo-deltoidal icositetrahedron | |
|---|---|
 | |
| Type | Johnson solid dual, Pseudo-uniform polyhedron dual |
| Faces |  24 kites |
| Edges | 48 |
| Vertices | 26 |
| Vertex configuration | (2) 4.4.4 (8+8+2) 4.4.4.4 |
| Symmetry group | Dihedral (D4d) |
| Dual polyhedron | Elongated square gyrobicupola |
| Properties | convex |
| Net | 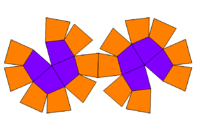 |
The pseudo-deltoidal icositetrahedron is a convex polyhedron with 24 kites as its faces. It is the dual of the pseudorhombicuboctahedron (also known as the elongated square gyrobicupola).
It is similar to the deltoidal icositetrahedron, but has a twist, similar to the relationship between the pseudorhombicuboctahedron and the rhombicuboctahedron. As the pseudorhombicuboctahedron is not truly vertex-transitive, the pseudo-deltoidal icositetrahedron is not truly face-transitive, with its faces in two different symmetry orbits (three if one only considers rotational symmetries); however, since the pseudorhombicuboctahedron has a singular vertex figure, the pseudo-deltoidal icositetrahedron has only one type of face (monohedral).
External links
This article is issued from Wikipedia - version of the Wednesday, August 19, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.