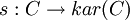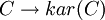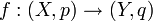Pseudo-abelian category
In mathematics, specifically in category theory, a pseudo-abelian category is a category that is preadditive and is such that every idempotent has a kernel
.[1] Recall that an idempotent morphism  is an endomorphism of an object with the property that
is an endomorphism of an object with the property that 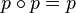 . Elementary considerations show that every idempotent then has a cokernel.[2] The pseudo-abelian condition is stronger than preadditivity, but it is weaker than the requirement that every morphism have a kernel and cokernel, as is true for abelian categories.
. Elementary considerations show that every idempotent then has a cokernel.[2] The pseudo-abelian condition is stronger than preadditivity, but it is weaker than the requirement that every morphism have a kernel and cokernel, as is true for abelian categories.
Synonyms in the literature for pseudo-abelian include pseudoabelian and Karoubian.
Examples
Any abelian category, in particular the category Ab of abelian groups, is pseudo-abelian. Indeed, in an abelian category, every morphism has a kernel.
The category of associative rngs (not rings!) together with multiplicative morphisms is pseudo-abelian.
A more complicated example is the category of Chow motives. The construction of Chow motives uses the pseudo-abelian completion described below.
Pseudo-abelian completion
The Karoubi envelope construction associates to an arbitrary category 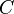 a category
a category 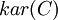 together with a functor
together with a functor
such that the image 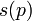 of every idempotent
of every idempotent  in
in 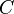 splits in
splits in 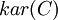 .
When applied to a preadditive category
.
When applied to a preadditive category 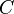 , the Karoubi envelope construction yields a pseudo-abelian category
, the Karoubi envelope construction yields a pseudo-abelian category 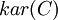 called the pseudo-abelian completion of
called the pseudo-abelian completion of 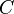 . Moreover, the functor
. Moreover, the functor
is in fact an additive morphism.
To be precise, given a preadditive category 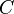 we construct a pseudo-abelian category
we construct a pseudo-abelian category 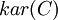 in the following way. The objects of
in the following way. The objects of 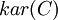 are pairs
are pairs 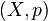 where
where  is an object of
is an object of 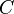 and
and  is an idempotent of
is an idempotent of  . The morphisms
. The morphisms
in 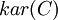 are those morphisms
are those morphisms
such that 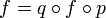 in
in 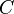 .
The functor
.
The functor
is given by taking  to
to 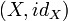 .
.
Citations
- ↑ Artin, 1972, p. 413.
- ↑ Lars Brünjes, Forms of Fermat equations and their zeta functions, Appendix A
References
- Artin, Michael; Alexandre Grothendieck, Jean-Louis Verdier, eds. (1972). Séminaire de Géométrie Algébrique du Bois Marie - 1963-64 - Théorie des topos et cohomologie étale des schémas - (SGA 4) - vol. 1 (Lecture notes in mathematics 269) (in French). Berlin; New York: Springer-Verlag. xix+525. Cite uses deprecated parameter
|coauthors=(help)