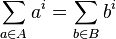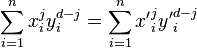Prouhet–Tarry–Escott problem
In mathematics, the Prouhet–Tarry–Escott problem asks for two disjoint sets A and B of n integers each, such that:
for each integer i from 1 to a given k.[1]
This problem was named after Eugène Prouhet, who studied it in the early 1850s, and Gaston Tarry and Escott, who studied it in the early 1910s. The problem originates from letters of Christian Goldbach and Leonhard Euler (1750/1751).
Examples
It has been shown that n must be strictly greater than k. The largest value of k for which a solution with n = k+1 is known is given by A = {±22, ±61, ±86, ±127, ±140, ±151}, B = {±35, ±47, ±94, ±121, ±146, ±148} for which k = 11.[2]
An example for n = 6 and k = 5 is given by the two sets { 0, 5, 6, 16, 17, 22 } and { 1, 2, 10, 12, 20, 21 }, because:
- 01 + 51 + 61 + 161 + 171 + 221 = 11 + 21 + 101 + 121 + 201 + 211
- 02 + 52 + 62 + 162 + 172 + 222 = 12 + 22 + 102 + 122 + 202 + 212
- 03 + 53 + 63 + 163 + 173 + 223 = 13 + 23 + 103 + 123 + 203 + 213
- 04 + 54 + 64 + 164 + 174 + 224 = 14 + 24 + 104 + 124 + 204 + 214
- 05 + 55 + 65 + 165 + 175 + 225 = 15 + 25 + 105 + 125 + 205 + 215.
Generalizations
A higher dimensional version of the Prouhet-Tarry-Escott problem has been introduced and studied by Andreas Alpers and Robert Tijdeman in 2007: Given parameters 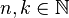 , find two different multi-sets
, find two different multi-sets  ,
, 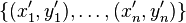 of points from
of points from 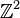 such that
such that
for all 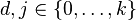 with
with 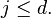 This problem is related to discrete tomography and also leads to Prouhet-Tarry-Escott solutions over the Gaussian integers.
This problem is related to discrete tomography and also leads to Prouhet-Tarry-Escott solutions over the Gaussian integers.
A solution for 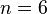 and
and 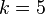 is given, for instance, by:
is given, for instance, by:
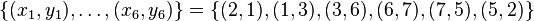 and
and
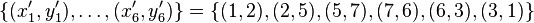 .
.
No solutions for 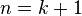 with
with 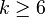 are known.
are known.
See also
- Thue–Morse sequence
- Euler's sum of powers conjecture
- Beal's conjecture
- Jacobi–Madden equation
- Taxicab number
- Pythagorean quadruple
- Sums of powers, a list of related conjectures and theorems
- Discrete tomography
Notes
References
- Borwein, Peter B. (2002), "The Prouhet–Tarry–Escott problem", Computational Excursions in Analysis and Number Theory, CMS Books in Mathematics, Springer-Verlag, pp. 85–96, ISBN 0-387-95444-9, retrieved 2009-06-16 Chap.11.
- Alpers, Andreas; Rob Tijdeman (2007), "The Two-Dimensional Prouhet-Tarry-Escott Problem" (PDF), Journal of Number Theory 123 (2): 403–412, doi:10.1016/j.jnt.2006.07.001, retrieved 2015-04-01.