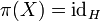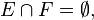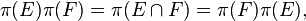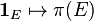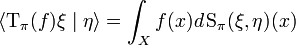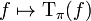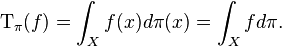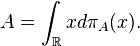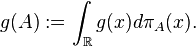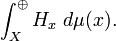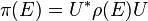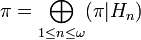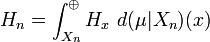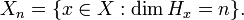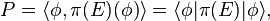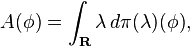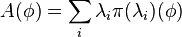Projection-valued measure

In mathematics, particularly in functional analysis, a projection-valued measure (PVM) is a function defined on certain subsets of a fixed set and whose values are self-adjoint projections on a fixed Hilbert space. Projection-valued measures are formally similar to real-valued measures, except that their values are self-adjoint projections rather than real numbers. As in the case of ordinary measures, it is possible to integrate complex-valued functions with respect to a PVM; the result of such an integration is a linear operator on the given Hilbert space.

Projection-valued measures are used to express results in spectral theory, such as the important spectral theorem for self-adjoint operators. The Borel functional calculus for self-adjoint operators is constructed using integrals with respect to PVMs. In quantum mechanics, PVMs are the mathematical description of projective measurements. They are generalized by positive operator valued measures (POVMs) in the same sense that a mixed state or density matrix generalizes the notion of a pure state.

Formal definition

A projection-valued measure on a measurable space (X, M), where M is a σ-algebra of subsets of X, is a mapping π from M to the set of self-adjoint projections on a Hilbert space H such that

\pi(X) = \operatorname{id}_H \quad

and for every ξ, η ∈ H, the set-function

E \mapsto \langle \pi(E)\xi \mid \eta \rangle

is a complex measure on M (that is, a complex-valued countably additive function). We denote this measure by 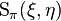$\operatorname{S}_\pi(\xi, \eta)$ . Note that 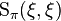$\operatorname{S}_\pi(\xi, \xi)$ is a real-valued measure, and a probability measure when $\xi$ has length one.

If π is a projection-valued measure and

E \cap F = \emptyset,

then π(E), π(F) are orthogonal projections. From this follows that in general,

\pi(E) \pi(F) = \pi(E \cap F) = \pi(F) \pi(E),

and they commute.

Example. Suppose (X, M, μ) is a measure space. Let π(E) be the operator of multiplication by the indicator function 1_E on L²(X). Then π is a projection-valued measure.

Extensions of projection-valued measures, integrals and the spectral theorem

If π is a projection-valued measure on (X, M), then the map

\mathbf{1}_E \mapsto \pi(E)

extends to a linear map on the vector space of step functions on X. In fact, it is easy to check that this map is a ring homomorphism. This map extends in a canonical way to all bounded complex-valued measurable functions on X, and we have the following.

Theorem. For any bounded M-measurable function f on X, there is a unique bounded linear operator T_π(f) such that

\langle \operatorname{T}_\pi(f) \xi \mid \eta \rangle = \int_X f(x) d \operatorname{S}_\pi (\xi,\eta)(x)

for all ξ, η ∈ H. Here, 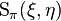$\operatorname{S}_\pi (\xi,\eta)$ denotes the complex measure 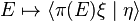$E \mapsto \langle \pi(E)\xi \mid \eta \rangle$ from the definition of 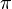$\pi$ . The map

f \mapsto \operatorname{T}_\pi(f)

is a homomorphism of rings. An integral notation is often used for 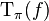$\operatorname{T}_\pi(f)$ , as in

\operatorname{T}_\pi(f)=\int_X f(x) d \pi(x) = \int_X f d \pi.

The theorem is also correct for unbounded measurable functions f, but then 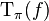$\operatorname{T}_\pi(f)$ will be an unbounded linear operator on the Hilbert space H.

The spectral theorem says that every self-adjoint operator 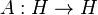$A:H\to H$ has an associated projection-valued measure $\pi_A$ defined on the real axis, such that

A =\int_\mathbb{R} x d \pi_A(x).

This allows to define the Borel functional calculus for such operators: if 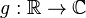$g:\mathbb{R}\to\mathbb{C}$ is a measurable function, we set

g(A) :=\int_\mathbb{R} g(x) d \pi_A(x).

Structure of projection-valued measures

First we provide a general example of projection-valued measure based on direct integrals. Suppose (X, M, μ) is a measure space and let {H_x}_{x ∈ X} be a μ-measurable family of separable Hilbert spaces. For every E ∈ M, let π(E) be the operator of multiplication by 1_E on the Hilbert space

\int_X^\oplus H_x \ d \mu(x).

Then π is a projection-valued measure on (X, M).

Suppose π, ρ are projection-valued measures on (X, M) with values in the projections of H, K. π, ρ are unitarily equivalent if and only if there is a unitary operator U:H → K such that

\pi(E) = U^* \rho(E) U \quad

for every E ∈ M.

Theorem. If (X, M) is a standard Borel space, then for every projection-valued measure π on (X, M) taking values in the projections of a separable Hilbert space, there is a Borel measure μ and a μ-measurable family of Hilbert spaces {H_x}_{x ∈ X}, such that π is unitarily equivalent to multiplication by 1_E on the Hilbert space

\int_X^\oplus H_x \ d \mu(x).

The measure class of μ and the measure equivalence class of the multiplicity function x → dim H_x completely characterize the projection-valued measure up to unitary equivalence.

A projection-valued measure π is homogeneous of multiplicity n if and only if the multiplicity function has constant value n. Clearly,

Theorem. Any projection-valued measure π taking values in the projections of a separable Hilbert space is an orthogonal direct sum of homogeneous projection-valued measures:

\pi = \bigoplus_{1 \leq n \leq \omega} (\pi | H_n)

where

H_n = \int_{X_n}^\oplus H_x \ d (\mu | X_n) (x)

and

X_n = \{x \in X: \operatorname{dim} H_x = n\}.

Application in quantum mechanics

In quantum mechanics, the unit sphere of the Hilbert space H is interpreted as the set of possible states Φ of a quantum system, the measurable space X is the value space for some quantum property of the system (an "observable"), and the projection-valued measure π expresses the probability that the observable takes on various values.

A common choice for X is the real numbers, but it may also be R³ (for position or momentum), a discrete set (for angular momentum, energy of a bound state, etc), or the 2-point set "true" and "false" for the truth-value of an arbitrary proposition about Φ.

Let E be a measurable subset of X and Φ a state in H, so that |Φ|=1. The probability that the observable takes its value in E given the system in state Φ is

P = \langle \phi,\pi(E)(\phi)\rangle = \langle \phi|\pi(E)|\phi\rangle,

where the latter notation is preferred in physics. We can parse this in two ways. First, for each fixed E, the projection π(E) is a self-adjoint operator on H whose 1-eigenspace is the states Φ for which the value of the observable always lies in E, and whose 0-eigenspace is the states Φ for which the value of the observable never lies in E. Second, for each fixed Φ, the association E ↦ ⟨Φ,π(⋅)Φ⟩ is a probability measure on X making the values of the observable into a random variable.

A measurement that can be performed by a projection-valued measure π is called a projective measurement. If X is the real numbers, there is associated to π a Hermitian operator A defined on H by

A(\phi) = \int_{\bold{R}} \lambda \,d\pi(\lambda)(\phi),

which takes the more readable form

A(\phi) = \sum_i \lambda_i \pi({\lambda_i})(\phi)

if the support of π is a discrete subset of R. This operator is called an observable in quantum mechanics.

Generalizations

The idea of a projection-valued measure is generalized by the positive operator-valued measure (POVM), where the need for the orthogonality implied by projection operators is replaced by the idea of a set of operators that are a non-orthogonal partition of unity. This generalization is motivated by applications to quantum information theory.

References

G. W. Mackey, The Theory of Unitary Group Representations, The University of Chicago Press, 1976
M. Reed and B. Simon, Methods of Mathematical Physics, vols I–IV, Academic Press 1972.
G. Teschl, Mathematical Methods in Quantum Mechanics with Applications to Schrödinger Operators, http://www.mat.univie.ac.at/~gerald/ftp/book-schroe/, American Mathematical Society, 2009.
V. S. Varadarajan, Geometry of Quantum Theory V2, Springer Verlag, 1970.

This article is issued from Wikipedia - version of the Monday, May 04, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.