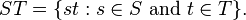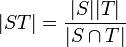Product of group subsets

In mathematics, one can define a product of group subsets in a natural way. If S and T are subsets of a group G, then their product is the subset of G defined by

ST = \{st : s \in S \text{ and } t\in T\}.

Note that S and T need not be subgroups for this product to be well defined. The associativity of this product follows from that of the group product. The product of group subsets therefore defines a natural monoid structure on the power set of G.

A lot more can be said in the case where S and T are subgroups.

Product of subgroups

If S and T are subgroups of G their product need not be a subgroup (consider, for example, two distinct subgroups of order two in the symmetric group on 3 symbols). This product is sometimes called the Frobenius product.[1] In general, the product of two subgroups S and T is a subgroup if and only if ST = TS,[2] and the two subgroups are said to permute. (Walter Ledermann has called this fact the Product Theorem,[3] but this name, just like "Frobenius product" is by no means standard.) In this case, ST is the group generated by S and T, i.e. ST = TS = ⟨S ∪ T⟩.

If either S or T is normal then the condition ST=TS is satisfied and the product is a subgroup.[4][5] If both S and T are normal, then the product is normal as well.[4]

If G is a finite group and S and T are subgroups of G, then ST is a subset of G of size |ST| given by the product formula:

|ST| = \frac{|S||T|}{|S\cap T|}

Note that this applies even if neither S nor T is normal.

Modular law

The following modular law (for groups) holds for any Q a subgroup of S, where T is any other arbitrary subgroup (and both S and T are subgroups of some group G):

Q(S ∩ T) = S ∩ (QT).

The two products that appear in this equality are not necessarily subgroups.

If QT is a subgroup (equivalently, as noted above, if Q and T permute) then QT = ⟨Q ∪ T⟩ = Q ∨ T, i.e. QT is the meet of Q and T in the lattice of subgroups of G, and the modular law for such a pair may also be written as Q ∨ (S ∩ T) = S ∩ (Q ∨ T), which is the equation that defines a modular lattice if it holds for any three elements of the lattice with Q ≤ S. In particular, since normal subgroups permute with each other, they form a modular sublattice.

A group in which every subgroup permutes is called an Iwasawa group. The subgroup lattice of an Iwasawa group is thus a modular lattice, so these groups are sometimes called modular groups[6] (although this latter term may have other meanings.)

The assumption in the modular law for groups (as formulated above) that Q is a subgroup of S is essential. If Q is not a subgroup of S, then the tentative, more general distributive property that one may consider S ∩ (QT) = (S ∩ Q)(S ∩ T) is false.[7][8]

Product of subgroups with trivial intersection

In particular, if S and T intersect only in the identity, then every element of ST has a unique expression as a product st with s in S and t in T. If S and T also commute, then ST is a group, and is called a Zappa–Szép product. Even further, if S or T is normal in ST, then ST coincides with the semidirect product of S and T. Finally, if both S and T are normal in ST, then ST coincides with the direct product of S and T.

If S and T are subgroups whose intersection is the trivial subgroup (identity element) and additionally ST=G, then S is called a complement of T and vice-versa.

By an abuse of terminology, two subgroups that intersect only in the identity are sometimes called disjoint.[9]

Product of subgroups with non-trivial intersection

A question that arises in the case of a non-trivial intersection between a normal subgroup N and a subgroup K is what is the structure of the quotient NK/N. Although one might be tempted to just "cancel out" N and say the answer is K, that is not correct because a homomorphism with kernel N will also "collapse" (map to 1) all elements of K that happen to be in N. Thus the correct answer is that NK/N is isomorphic with K/(N∩K). This fact is sometimes called the second isomorphism theorem,[10] (although the numbering of these theorems sees some variation between authors); it is has also been called the diamond theorem by I. Martin Isaacs because of the shape of subgroup lattice involved,[11] and has also been called the parallelogram rule by Paul Moritz Cohn, who thus emphasized analogy with the parallelogram rule for vectors because in the resulting subgroup lattice the two sides assumed to represent the quotient groups (SN) / N and S / (S ∩ N) are "equal" in the sense of isomorphism.[8]

Frattini's argument guarantees the existence of a product of subgroups (giving rise to the whole group) in a case where the intersection is not necessarily trivial (and for this latter reason the two subgroups are not complements). More specifically, if G is a finite group with normal subgroup N, and if P is a Sylow p-subgroup of N, then G = NG(P)N, where NG(P) denotes the normalizer of P in G. (Note that the normalizer of P includes P, so the intersection between N and NG(P) is at least P.)

Generalization to semigroups

In a semigroup, the product of two subsets is always a subsemigroup; furthermore the power set of subsemigroups is a semiring with addition as union (of subsets) and multiplication as product of subsets.[12]

See also

References

  1. ↑ Adolfo Ballester-Bolinches; Ramon Esteban-Romero; Mohamed Asaad (2010). Products of Finite Groups. Walter de Gruyter. p. 1. ISBN 978-3-11-022061-2.
  2. ↑ W. Keith Nicholson (2012). Introduction to Abstract Algebra (4th ed.). John Wiley & Sons. Lemma 2, p. 125. ISBN 978-1-118-13535-8.
  3. ↑ Walter Ledermann, Introduction to Group Theory, 1976, Longman, ISBN 0-582-44180-3, p. 52
  4. 1 2 Nicholson, 2012, Theorem 5, p. 125
  5. ↑ David A.R. Wallace (1998). Groups, Rings and Fields. Springer Science & Business Media. Theorem 14, p. 123. ISBN 978-3-540-76177-8.
  6. ↑ Ballester-Bolinches, Esteban-Romero, Asaad, p. 24
  7. ↑ Derek Robinson (1996). A Course in the Theory of Groups. Springer Science & Business Media. p. 15. ISBN 978-0-387-94461-6.
  8. 1 2 Paul Moritz Cohn (2000). Classic algebra. Wiley. p. 248. ISBN 978-0-471-87731-8.
  9. ↑ L. Fuchs (1970). Infinite Abelian Groups. Volume I. Academic Press. p. 37. ISBN 978-0-08-087348-0.
  10. ↑ Dan Saracino (1980). Abstract Algebra: A First Course. Addison-Wesley. p. 123. ISBN 0-201-07391-9.
  11. ↑ I. Martin Isaacs (1994). Algebra: A Graduate Course. American Mathematical Soc. p. 33. ISBN 978-0-8218-4799-2.
  12. ↑ Jean E. Pin (1989). Formal Properties of Finite Automata and Applications: LITP Spring School on Theoretical Computer Science, Ramatuelle, France, May 23–27, 1988. Proceedings. Springer Science & Business Media. p. 35. ISBN 978-3-540-51631-6.
This article is issued from Wikipedia - version of the Saturday, January 30, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.