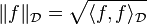Product distribution
A product distribution is a probability distribution constructed as the distribution of the product of random variables having two other known distributions. Given two statistically independent random variables X and Y, the distribution of the random variable Z that is formed as the product
is a product distribution.
Algebra of random variables
The product is one type of algebra for random variables: Related to the product distribution are the ratio distribution, sum distribution (see List of convolutions of probability distributions) and difference distribution. More generally, one may talk of combinations of sums, differences, products and ratios.
Many of these distributions are described in Melvin D. Springer's book from 1979 The Algebra of Random Variables.[1]
Derivation for independent random variables
If  and
and 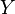 are two independent, continuous random variables, described by probability density functions
are two independent, continuous random variables, described by probability density functions  and
and 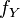 then the probability density function of
then the probability density function of  is[2]
is[2]
Proof [3]
First note that
Then define the variable transformation  which has the inverse
which has the inverse 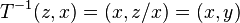 . The Jacobian is given by
. The Jacobian is given by
Equipped with this we obtain finally for the above probability, the following double integral
and thus after changing the order of integration finally
and the inner integral is just the desired probability density function.
Expectation of product of random variables
When two random variables are statistically independent, the expectation of their product is the product of their expectations. This can be proved from the Law of total expectation:
In the inner expression, Y is a constant. Hence:
This is true even if X and Y are statistically dependent. However, in general ![\operatorname{E}_{X\mid Y}[X]](../I/m/33f96a97655899239e6a0b86fb640ba7.png) is a function of Y. In the special case in which X and Y are statistically
independent, it is a constant independent of Y. Hence:
is a function of Y. In the special case in which X and Y are statistically
independent, it is a constant independent of Y. Hence:
Special cases
The distribution of the product of two random variables which have lognormal distributions is again lognormal. This is itself a special case of a more general set of results where the logarithm of the product can be written as the sum of the logarithms. Thus, in cases where a simple result can be found in the list of convolutions of probability distributions, where the distributions to be convolved are those of the logarithms of the components of the product, the result might be transformed to provide the distribution of the product. However this approach is only useful where the logarithms of the components of the product are in some standard families of distributions.
The distribution of the product of a random variable having a uniform distribution on (0,1) with a random variable having a gamma distribution with shape parameter equal to 2, is an exponential distribution.[4] A more general case of this concerns the distribution of the product of a random variable having a beta distribution with a random variable having a gamma distribution: for some cases where the parameters of the two component distributions are related in a certain way, the result is again a gamma distribution but with a changed shape parameter.[4]
The K-distribution is an example of a non-standard distribution that can be defined as a product distribution (where both components have a gamma distribution).
In theoretical computer science
In computational learning theory, a product distribution 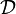 over
over 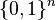 is specified by the parameters
is specified by the parameters
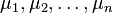 . Each parameter
. Each parameter  gives the marginal probability that the ith bit of
gives the marginal probability that the ith bit of
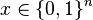 sampled as
sampled as  is 1; i.e.
is 1; i.e.
![\mu_i = \operatorname{Pr}_{\mathcal{D}}[x_i = 1]](../I/m/30551b312fedc6062463d4397b93622d.png) . In this setting, the uniform distribution is simply a product distribution with every
. In this setting, the uniform distribution is simply a product distribution with every 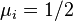 .
.
Product distributions are a key tool used for proving learnability results when the examples cannot be assumed to be uniformly sampled.[5] They give rise to an inner product
 on the space of real-valued functions on
on the space of real-valued functions on 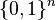 as follows:
as follows:
This inner product gives rise to a corresponding norm as follows:
See also
Notes
- ↑ Springer, Melvin Dale (1979). The Algebra of Random Variables. Wiley. ISBN 0-471-01406-0. Retrieved 24 September 2012.
- ↑ Rohatgi, V. K. (1976). An Introduction to Probability Theory and Mathematical Statistics. New York: Wiley. ISBN 0-19-853185-0. Retrieved 4 October 2015.
- ↑ Grimmett, G. R.; Stirzaker, D.R. (2001). Probability and Random Processes. Oxford: Oxford University Press. ISBN 978-0-19-857222-0. Retrieved 4 October 2015.
- 1 2 Johnson, Norman L.; Kotz, Samuel; Balakrishnan, N. (1995). Continuous Univariate Distributions Volume 2, Second edition. Wiley. p. 306. ISBN 0-471-58494-0. Retrieved 24 September 2012.
- ↑ Servedio, Rocco A. (2004), "On learning monotone DNF under product distributions", Inf. Comput. (Academic Press, Inc.) 193 (1): 57–74, doi:10.1016/j.ic.2004.04.003
References
- Springer, Melvin Dale; Thompson, W. E. (1970). "The distribution of products of beta, gamma and Gaussian random variables". SIAM Journal on Applied Mathematics 18 (4): 721–737. doi:10.1137/0118065. JSTOR 2099424.
- Springer, Melvin Dale; Thompson, W. E. (1966). "The distribution of products of independent random variables". SIAM Journal on Applied Mathematics 14 (3): 511–526. doi:10.1137/0114046. JSTOR 2946226.

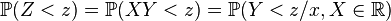
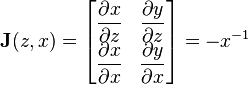


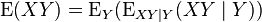
![\operatorname{E}_{X Y \mid Y} (X Y \mid Y) = Y\cdot \operatorname{E}_{X\mid Y}[X]](../I/m/9753537f15b8625236edc04ad5c3e01d.png)
![\operatorname{E}(X Y) = \operatorname{E}_Y ( Y\cdot \operatorname{E}_{X\mid Y}[X])](../I/m/ebd8fb54188536ec97ea36e4180a25c0.png)
![\operatorname{E}(X Y) = \operatorname{E}_Y ( Y\cdot \operatorname{E}_{X}[X])](../I/m/9ba1d79875c184a7ab866984c73badb0.png)
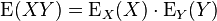
![\langle f, g \rangle_\mathcal{D} = \sum_{x \in \{0,1\}^n} \mathcal{D}(x)f(x)g(x) = \mathbb{E}_{\mathcal{D}} [fg]](../I/m/af9e3a501f9c3072b478e4e9ab56723c.png)