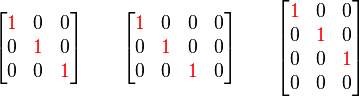Main diagonal

In linear algebra, the main diagonal (sometimes principal diagonal, primary diagonal, leading diagonal, or major diagonal) of a matrix A is the collection of entries A_{i,j} where i = j. The following three matrices have their main diagonals indicated by red 1's:

\begin{bmatrix} \color{red}{1} & 0 & 0\\ 0 & \color{red}{1} & 0\\ 0 & 0 & \color{red}{1}\end{bmatrix} \qquad \begin{bmatrix} \color{red}{1} & 0 & 0 & 0 \\ 0 & \color{red}{1} & 0 & 0 \\ 0 & 0 & \color{red}{1} & 0 \end{bmatrix} \qquad \begin{bmatrix} \color{red}{1} & 0 & 0\\ 0 & \color{red}{1} & 0\\ 0 & 0 & \color{red}{1}\\ 0 & 0 & 0\end{bmatrix}

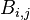The antidiagonal (sometimes counterdiagonal, secondary diagonal, trailing diagonal or minor diagonal) of a dimension N square matrix, B, is the collection of entries B_{i,j} such that 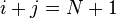i + j = N + 1. That is, it runs from the top right corner to the bottom left corner:

\begin{bmatrix} 0 & 0 & \color{red}{1}\\ 0 & \color{red}{1} & 0\\ \color{red}{1} & 0 & 0\end{bmatrix}

See also

References

This article is issued from Wikipedia - version of the Monday, November 16, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.