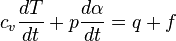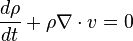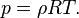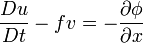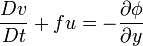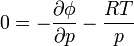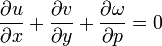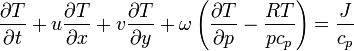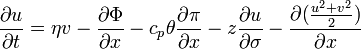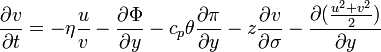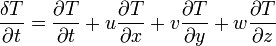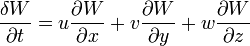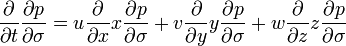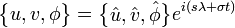Primitive equations
The primitive equations are a set of nonlinear differential equations that are used to approximate global atmospheric flow and are used in most atmospheric models. They consist of three main sets of balance equations:
- A continuity equation: Representing the conservation of mass.
- Conservation of momentum: Consisting of a form of the Navier–Stokes equations that describe hydrodynamical flow on the surface of a sphere under the assumption that vertical motion is much smaller than horizontal motion (hydrostasis) and that the fluid layer depth is small compared to the radius of the sphere
- A thermal energy equation: Relating the overall temperature of the system to heat sources and sinks
The primitive equations may be linearized to yield Laplace's tidal equations, an eigenvalue problem from which the analytical solution to the latitudinal structure of the flow may be determined.
In general, nearly all forms of the primitive equations relate the five variables u, v, ω, T, W, and their evolution over space and time.
The equations were first written down by Vilhelm Bjerknes.[1]
Definitions
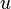 is the zonal velocity (velocity in the east/west direction tangent to the sphere)
is the zonal velocity (velocity in the east/west direction tangent to the sphere)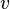 is the meridional velocity (velocity in the north/south direction tangent to the sphere)
is the meridional velocity (velocity in the north/south direction tangent to the sphere)- ω is the vertical velocity in isobaric coordinates
 is the temperature
is the temperature- Φ is the geopotential
 is the term corresponding to the Coriolis force, and is equal to
is the term corresponding to the Coriolis force, and is equal to 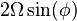 , where
, where  is the angular rotation rate of the Earth (
is the angular rotation rate of the Earth (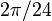 radians per sidereal hour), and
radians per sidereal hour), and  is the latitude
is the latitude is the gas constant
is the gas constant is the pressure
is the pressure is the specific heat on a constant pressure surface
is the specific heat on a constant pressure surface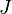 is the heat flow per unit time per unit mass
is the heat flow per unit time per unit mass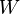 is the precipitable water
is the precipitable water- Π is the Exner function
 is the potential temperature
is the potential temperature
Forces that cause atmospheric motion
Forces that cause atmospheric motion include the pressure gradient force, gravity, and viscous friction. Together, they create the forces that accelerate our atmosphere.
The pressure gradient force causes an acceleration forcing air from regions of high pressure to regions of low pressure. Mathematically, this can be written as:
The gravitational force accelerates objects at approximately 9.81 m/s2 directly towards the center of the Earth.
The force due to viscous friction can be approximated as:
Using Newton's second law, these forces (referenced in the equations above as the accelerations due to these forces) may be summed to produce an equation of motion that describes this system. This equation can be written in the form:
Therefore, to complete the system of equations and obtain 6 equations and 6 variables:
Forms of the primitive equations
The precise form of the primitive equations depends on the vertical coordinate system chosen, such as pressure coordinates, log pressure coordinates, or sigma coordinates. Furthermore, the velocity, temperature, and geopotential variables may be decomposed into mean and perturbation components using Reynolds decomposition.
Vertical pressure, Cartesian tangential plane
In this form pressure is selected as the vertical coordinate and the horizontal coordinates are written for the Cartesian tangential plane (i.e. a plane tangent to some point on the surface of the Earth). This form does not take the curvature of the Earth into account, but is useful for visualizing some of the physical processes involved in formulating the equations due to its relative simplicity.
Note that the capital derivatives are the material derivatives.
- the geostrophic momentum equations
- the hydrostatic equation, a special case of the vertical momentum equation in which there is no background vertical acceleration.
- the continuity equation, connecting horizontal divergence/convergence to vertical motion under the hydrostatic approximation (
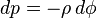 ):
):
- and the thermodynamic energy equation, a consequence of the first law of thermodynamics
When a statement of the conservation of water vapor substance is included, these six equations form the basis for any numerical weather prediction scheme.
Primitive equations using sigma coordinate system, polar stereographic projection
According to the National Weather Service Handbook No. 1 – Facsimile Products, the primitive equations can be simplified into the following equations:
- Zonal wind:
- Meridional wind:
- Temperature:
The first term is equal to the change in temperature due to incoming solar radiation and outgoing longwave radiation, which changes with time throughout the day. The second, third, and fourth terms are due to advection. Additionally, the variable T with subscript is the change in temperature on that plane. Each T is actually different and related to its respective plane. This is divided by the distance between grid points to get the change in temperature with the change in distance. When multiplied by the wind velocity on that plane, the units kelvins per meter and meters per second give kelvins per second. The sum of all the changes in temperature due to motions in the x, y, and z directions give the total change in temperature with time.
- Precipitable water:
This equation and notation works in much the same way as the temperature equation. This equation describes the motion of water from one place to another at a point without taking into account water that changes form. Inside a given system, the total change in water with time is zero. However, concentrations are allowed to move with the wind.
- Pressure thickness:
These simplifications make it much easier to understand what is happening in the model. Things like the temperature (potential temperature), precipitable water, and to an extent the pressure thickness simply move from one spot on the grid to another with the wind. The wind is forecast slightly differently. It uses geopotential, specific heat, the exner function π, and change in sigma coordinate.
Solution to the linearized primitive equations
The analytic solution to the linearized primitive equations involves a sinusoidal oscillation in time and longitude, modulated by coefficients related to height and latitude.
where s and 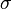 are the zonal wavenumber and angular frequency, respectively. The solution represents atmospheric waves and tides.
are the zonal wavenumber and angular frequency, respectively. The solution represents atmospheric waves and tides.
When the coefficients are separated into their height and latitude components, the height dependence takes the form of propagating or evanescent waves (depending on conditions), while the latitude dependence is given by the Hough functions.
This analytic solution is only possible when the primitive equations are linearized and simplified. Unfortunately many of these simplifications (i.e. no dissipation, isothermal atmosphere) do not correspond to conditions in the actual atmosphere. As a result, a numerical solution which takes these factors into account is often calculated using general circulation models and climate models.
See also
- Barometric formula
- Climate model
- Euler equations
- Fluid dynamics
- General circulation model
- Numerical weather prediction
References
- Beniston, Martin. From Turbulence to Climate: Numerical Investigations of the Atmosphere with a Hierarchy of Models. Berlin: Springer, 1998.
- Firth, Robert. Mesoscale and Microscale Meteorological Model Grid Construction and Accuracy. LSMSA, 2006.
- Thompson, Philip. Numerical Weather Analysis and Prediction. New York: The Macmillan Company, 1961.
- Pielke, Roger A. Mesoscale Meteorological Modeling. Orlando: Academic Press, Inc., 1984.
- U.S. Department of Commerce, National Oceanic and Atmospheric Administration, National Weather Service. National Weather Service Handbook No. 1 – Facsimile Products. Washington, DC: Department of Commerce, 1979.
External links
National Weather Service – NCSU Collaborative Research and Training Site, Review of the Primitive Equations.
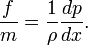
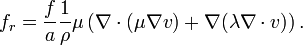
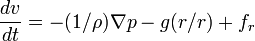
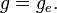
![\frac{dv}{dt} = - (1/\rho)\nabla p - g(r/r) + (1/\rho)\left[\nabla\cdot (\mu \nabla v) + \nabla(\lambda \nabla\cdot v)\right]](../I/m/f47b06326e579fbc6be56efb1931fb0f.png)