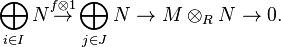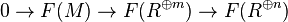Free presentation

In algebra, a free presentation of a module M over a commutative ring R is an exact sequence of R-modules:

\bigoplus_{i \in I} R \overset{f} \to \bigoplus_{j \in J} R \overset{g}\to M \to 0.

Note g then maps each basis element to each generator of M. In particular, if J is finite, then M is a finitely generated module. If I and J are finite sets, then the presentation is called a finite presentation; a module is called finitely presented if it admits a finite presentation.

A free presentation always exists: any module is a quotient of free module: 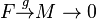F \overset{g}\to M \to 0, but then the kernel of g is again a quotient of a free module: 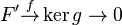F' \overset{f} \to \ker g \to 0. The combination of f and g is a free presentation of M. Now, one can obviously keep "resolving" the kernels in this fashion; the result is called a free resolution. Thus, a free presentation is the early part of the free resolution.

A presentation is useful for computaion. For example, since tensoring is right-exact, tensoring the above presentation with a module, say, N gives:

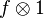\bigoplus_{i \in I} N \overset{f \otimes 1} \to \bigoplus_{j \in J} N \to M \otimes_R N \to 0.

This says that M \otimes_R N is the cokernel of f \otimes 1. If N is an R-algebra, then this is the presentation of the N-module M \otimes_R N; that is, the presentation extends under base extension.

For left-exact functors, there is for example

Proposition — Let F, G be left-exact contravariant functors from the category of modules over a commutative ring R to abelian groups and θ a natural transformation from F to G. If 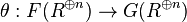\theta: F(R^{\oplus n}) \to G(R^{\oplus n}) is an isomorphism for each natural number n, then 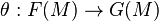\theta: F(M) \to G(M) is an isomorphism for any finitely-presented module M.

Proof: Applying F to a finite presentation 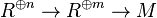R^{\oplus n} \to R^{\oplus m} \to M results in

0 \to F(M) \to F(R^{\oplus m}) \to F(R^{\oplus n})

and the same for G. Now apply the snake lemma. \square

See also

References


This article is issued from Wikipedia - version of the Saturday, October 17, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.