Preimage theorem
In mathematics, particularly in differential topology, the preimage theorem is a variation of the implicit function theorem concerning the preimage of particular points in a manifold under the action of a smooth map.[1][2]
Statement of Theorem
Definition. Let 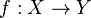 be a smooth map between manifolds. We say that a point
be a smooth map between manifolds. We say that a point  is a regular value of f if for all
is a regular value of f if for all  the map
the map  is surjective. Here,
is surjective. Here, 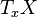 and
and 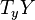 are the tangent spaces of X and Y at the points x and y.
are the tangent spaces of X and Y at the points x and y.
Theorem. Let 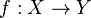 be a smooth map, and let
be a smooth map, and let  be a regular value of f; then
be a regular value of f; then 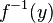 is a submanifold of X. If
is a submanifold of X. If  , then the codimension of
, then the codimension of 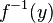 is equal to the dimension of Y. Also, the tangent space of
is equal to the dimension of Y. Also, the tangent space of 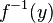 at
at  is equal to
is equal to 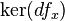 .
.
References
- ↑ Tu, Loring W. (2010), "9.3 The Regular Level Set Theorem", An Introduction to Manifolds, Springer, pp. 105–106, ISBN 9781441974006.
- ↑ Banyaga, Augustin (2004), "Corollary 5.9 (The Preimage Theorem)", Lectures on Morse Homology, Texts in the Mathematical Sciences 29, Springer, p. 130, ISBN 9781402026959.
This article is issued from Wikipedia - version of the Saturday, January 03, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.