Pregeometry (model theory)
Pregeometry, and in full combinatorial pregeometry, are essentially synonyms for "matroid". They were introduced by G.-C. Rota with the intention of providing a less "ineffably cacophonous" alternative term. Also, the term combinatorial geometry, sometimes abbreviated to geometry, was intended to replace "simple matroid". These terms are now infrequently used in the study of matroids.
In the branch of mathematical logic called model theory, infinite finitary matroids, there called "pregeometries" (and "geometries" if they are simple matroids), are used in the discussion of independence phenomena.
It turns out that many fundamental concepts of linear algebra – closure, independence, subspace, basis, dimension – are preserved in the framework of abstract geometries.
The study of how pregeometries, geometries, and abstract closure operators influence the structure of first-order models is called geometric stability theory.
Definitions
Pregeometries and geometries
A combinatorial pregeometry (also known as a finitary matroid), is a second-order structure: 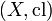 , where
, where 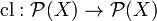 (called the closure map) satisfies the following axioms. For all
(called the closure map) satisfies the following axioms. For all 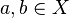 and
and 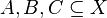 :
:
-
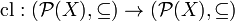 is an homomorphism in the category of partial orders (monotone increasing), and dominates
is an homomorphism in the category of partial orders (monotone increasing), and dominates 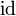 (I.e.
(I.e.  implies
implies  .) and is idempotent.
.) and is idempotent. - Finite character: For each
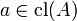 there is some finite
there is some finite 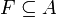 with
with 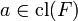 .
. - Exchange principle: If
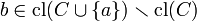 , then
, then 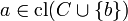 (and hence by monotonicity and idempotence in fact
(and hence by monotonicity and idempotence in fact 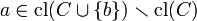 ).
).
A geometry is a pregeometry in which The closure of singletons are singletons and the closure of the empty set is the empty set.
Independence, bases and dimension
Given sets 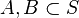 ,
,  is independent over
is independent over  if
if 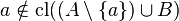 for any
for any  .
.
A set 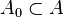 is a basis for
is a basis for  over
over  if it is independent over
if it is independent over  and
and 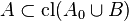 .
.
Since a pregeometry satisfies the Steinitz exchange property all bases are of the same cardinality, hence the definition of the dimension of  over
over  as
as 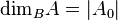 has no ambiguity.
has no ambiguity.
The sets  are independent over
are independent over 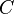 if
if 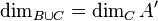 whenever
whenever  is a finite subset of
is a finite subset of  . Note that this relation is symmetric.
. Note that this relation is symmetric.
In minimal sets over stable theories the independence relation coincides with the notion of forking independence.
Geometry automorphism
A geometry automorphism of a geometry 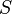 is a bijection
is a bijection 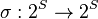 such that
such that 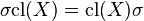 for any
for any 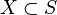 .
.
A pregeometry 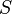 is said to be homogeneous if for any closed
is said to be homogeneous if for any closed 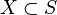 and any two elements
and any two elements 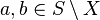 there is an automorphism of
there is an automorphism of 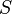 which maps
which maps  to
to  and fixes
and fixes  pointwise.
pointwise.
The associated geometry and localizations
Given a pregeometry 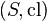 its associated geometry (sometimes referred in the literature as the canonical geometry) is the geometry
its associated geometry (sometimes referred in the literature as the canonical geometry) is the geometry 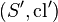 where
where
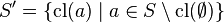 , and
, and- For any
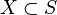 ,
, 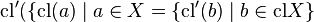
Its easy to see that the associated geometry of a homogeneous pregeometry is homogeneous.
Given 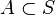 the localization of
the localization of 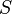 is the geometry
is the geometry 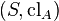 where
where 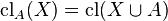 .
.
Types of pregeometries
Let 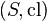 be a pregeometry, then it is said to be:
be a pregeometry, then it is said to be:
- trivial (or degenerate) if
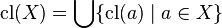 ,
, - modular if any two closed finite dimensional sets
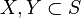 satisfy the equation
satisfy the equation 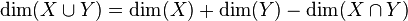 (or equivalently that
(or equivalently that  is independent of
is independent of 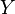 over
over 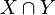 .
. - locally modular if it has a localization at a singleton which is modular
4. (locally) projective if it is non-trivial and (locally) modular 5. locally finite if closures of finite sets are finite
Triviality, modularity and local modularity pass to the associated geometry and are preserved under localization.
If 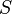 is a locally modular homogeneous pregeometry and
is a locally modular homogeneous pregeometry and 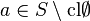 then the localization of
then the localization of 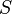 in
in  is modular.
is modular.
The geometry 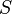 is modular if and only if whenver
is modular if and only if whenver 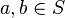 ,
, 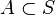 ,
, 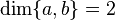 and
and 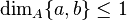 then
then 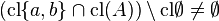 .
.
Examples
The trivial example
If 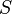 is any set we may define
is any set we may define 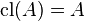 . This pregeometry is a trivial, homogeneous, locally finite geometry.
. This pregeometry is a trivial, homogeneous, locally finite geometry.
Vector spaces and projective spaces
Let  be a field (a division ring actually suffices) and let
be a field (a division ring actually suffices) and let  be a
be a 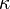 -dimensional vector space over
-dimensional vector space over  . Then
. Then  is a pregeometry where closures of sets are defined to be their span.
is a pregeometry where closures of sets are defined to be their span.
This pregeometry is homogeneous and modular. Vector spaces are considered to be the prototypical example of modularity.
 is locally finite if and only if
is locally finite if and only if  is finite.
is finite.
 is not a geometry, as the closure of any nontrivial vector is a subspace of size at least
is not a geometry, as the closure of any nontrivial vector is a subspace of size at least 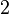 .
.
The associated geometry of a 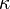 -dimensional vector space over
-dimensional vector space over  is the
is the 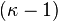 -dimensional projective space over
-dimensional projective space over  . It is easy to see that this pregeometry is a projective geometry.
. It is easy to see that this pregeometry is a projective geometry.
Affine spaces
Let  be a
be a 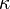 -dimensional affine space over a field
-dimensional affine space over a field  . Given a set define its closure to be its affine hull (i.e. the smallest affine subspace containing it).
. Given a set define its closure to be its affine hull (i.e. the smallest affine subspace containing it).
This forms a homogeneous 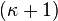 -dimensional geometry.
-dimensional geometry.
An affine space is not modular (for example, if  and
and 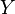 be parallel lines then the formula in the definition of modularity fails). However, it is easy to check that all localizations are modular.
be parallel lines then the formula in the definition of modularity fails). However, it is easy to check that all localizations are modular.
Algebraically closed fields
Let  be an algebraically closed field with
be an algebraically closed field with 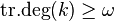 , and define the closure of a set to be its algebraic closure.
, and define the closure of a set to be its algebraic closure.
While vector spaces are modular and affine spaces are "almost" modular (i.e. everywhere locally modulare), algebraically closed fields are examples of the other extremity, not being even locally modular (i.e. none of the localizations is modular).
References
H.H. Crapo and G.-C. Rota (1970), On the Foundations of Combinatorial Theory: Combinatorial Geometries. M.I.T. Press, Cambridge, Mass.
Pillay, Anand (1996), Geometric Stability Theory. Oxford Logic Guides. Oxford University Press.