Predictable process

In stochastic analysis, a part of the mathematical theory of probability, a predictable process is a stochastic process whose value is knowable at a prior time. The predictable processes form the smallest class that is closed under taking limits of sequences and contains all adapted left-continuous processes.

Mathematical definition

Discrete-time process

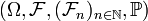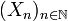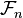Given a filtered probability space $(\Omega,\mathcal{F},(\mathcal{F}_n)_{n \in \mathbb{N}},\mathbb{P})$ , then a stochastic process $(X_n)_{n \in \mathbb{N}}$ is predictable if $X_{n+1}$ is measurable with respect to the σ-algebra $\mathcal{F}_n$ for each n.^[1]

Continuous-time process

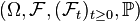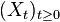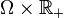Given a filtered probability space $(\Omega,\mathcal{F},(\mathcal{F}_t)_{t \geq 0},\mathbb{P})$ , then a continuous-time stochastic process $(X_t)_{t \geq 0}$ is predictable if $X$ , considered as a mapping from $\Omega \times \mathbb{R}_{+}$ , is measurable with respect to the σ-algebra generated by all left-continuous adapted processes.^[2]

Examples

Every deterministic process is a predictable process.
Every continuous-time adapted process that is left continuous is a predictable process.

References

↑ van Zanten, Harry (November 8, 2004). "An Introduction to Stochastic Processes in Continuous Time" (pdf). Retrieved October 14, 2011.
↑ "Predictable processes: properties" (pdf). Retrieved October 15, 2011.

This article is issued from Wikipedia - version of the Friday, February 27, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.