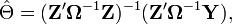Prais–Winsten estimation
In econometrics, Prais–Winsten estimation is a procedure meant to take care of the serial correlation of type AR(1) in a linear model. Conceived by Sigbert Prais and Christopher Winsten in 1954, it is a modification of Cochrane–Orcutt estimation in the sense that it does not lose the first observation and leads to more efficiency as a result.
Theory
Consider the model
where  is the time series of interest at time t,
is the time series of interest at time t, 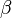 is a vector of coefficients,
is a vector of coefficients,  is a matrix of explanatory variables, and
is a matrix of explanatory variables, and  is the error term. The error term can be serially correlated over time:
is the error term. The error term can be serially correlated over time:  and
and 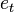 is a white noise. In addition to the Cochrane–Orcutt procedure transformation, which is
is a white noise. In addition to the Cochrane–Orcutt procedure transformation, which is
for t=2,3,...,T, Prais-Winsten procedure makes a reasonable transformation for t=1 in the following form
Then the usual least squares estimation is done.
Estimation procedure
To do the estimation in a compact way it is directive to look at the auto-covariance function of the error term considered in the model above:
Now is easy to see that the variance–covariance matrix,  , of the model is
, of the model is
Now having  (or an estimate of it), we see that,
(or an estimate of it), we see that,
where 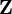 is a matrix of observations on the independent variable (Xt, t = 1, 2, ..., T) including a vector of ones,
is a matrix of observations on the independent variable (Xt, t = 1, 2, ..., T) including a vector of ones, 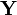 is a vector stacking the observations on the dependent variable (Xt, t = 1, 2, ..., T) and
is a vector stacking the observations on the dependent variable (Xt, t = 1, 2, ..., T) and  includes the model parameters.
includes the model parameters.
Note
To see why the initial observation assumption stated by Prais–Winsten (1954) is reasonable, considering the mechanics of general least square estimation procedure sketched above is helpful. The inverse of  can be decomposed as
can be decomposed as  with
with
A pre-multiplication of model in a matrix notation with this matrix gives the transformed model of Prais–Winsten.
Restrictions
The error term is still restricted to be of an AR(1) type. If  is not known, a recursive procedure may be used to make the estimation feasible. See Cochrane–Orcutt estimation.
is not known, a recursive procedure may be used to make the estimation feasible. See Cochrane–Orcutt estimation.
References
- Judge, George G.; Griffiths, William E.; Hill, R. Carter; Lee, Tsoung-Chao (1980). The Theory and Practice of Econometrics. New York: Wiley. pp. 180–183. ISBN 0-471-05938-2.
- Kmenta, Jan (1986). Elements of Econometrics (Second ed.). New York: Macmillan. pp. 302–320. ISBN 0-02-365070-2.
- Prais, S. J.; Winsten, C. B. (1954). "Trend Estimators and Serial Correlation" (PDF). Cowles Commission Discussion Paper No. 383 (Chicago).
- Wooldridge, J. (2008). Introductory Econometrics: A Modern Approach (4th ed.). South-Western. p. 435. ISBN 0-324-66054-5.

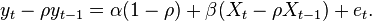


![\mathbf{\Omega} = \begin{bmatrix}
\frac{1}{1-\rho^2} & \frac{\rho}{1-\rho^2} & \frac{\rho^2}{1-\rho^2} & \cdots & \frac{\rho^{T-1}}{1-\rho^2} \\[8pt]
\frac{\rho}{1-\rho^2} & \frac{1}{1-\rho^2} & \frac{\rho}{1-\rho^2} & \cdots & \frac{\rho^{T-2}}{1-\rho^2} \\[8pt]
\frac{\rho^2}{1-\rho^2} & \frac{\rho}{1-\rho^2} & \frac{1}{1-\rho^2} & \cdots & \frac{\rho^{T-2}}{1-\rho^2} \\[8pt]
\vdots & \vdots & \vdots & \ddots & \vdots \\[8pt]
\frac{\rho^{T-1}}{1-\rho^2} & \frac{\rho^{T-2}}{1-\rho^2} & \frac{\rho^{T-3}}{1-\rho^2} & \cdots & \frac{1}{1-\rho^2}
\end{bmatrix}.](../I/m/6323f2842a05a3a1e1a7ad6c8e627bf0.png)