Monogenic field

In mathematics, a monogenic field is an algebraic number field K for which there exists an element a such that the ring of integers O_K is the polynomial ring Z[a]. The powers of such an element a constitute a power integral basis.

In a monogenic field K, the field discriminant of K is equal to the discriminant of the minimal polynomial of α.

Examples

Examples of monogenic fields include:

Quadratic fields:

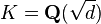K = \mathbf{Q}(\sqrt d)

with

d

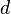a square-free integer, then

O_K = \mathbf{Z}[a]

where

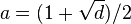a = (1+\sqrt d)/2

if d≡1 (mod 4) and

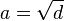a = \sqrt d

if d ≡ 2 or 3 (mod 4).

Cyclotomic fields:

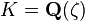K = \mathbf{Q}(\zeta)

with

\zeta

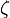a root of unity, then

O_K = \mathbf{Z}[\zeta].

Also the maximal real subfield

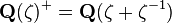\mathbf{Q}(\zeta)^{+} = \mathbf{Q}(\zeta + \zeta^{-1})

is monogenic, with ring of integers

\mathbf{Z}[\zeta+\zeta^{-1}].

While all quadratic fields are monogenic, already among cubic fields there are many that are not monogenic. The first example of a non-monogenic number field that was found is the cubic field generated by a root of the polynomial 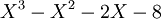$X^3 - X^2 - 2X - 8$ , due to Richard Dedekind.

References

Narkiewicz, Władysław (2004). Elementary and Analytic Theory of Algebraic Numbers (3rd ed.). Springer-Verlag. p. 64. ISBN 3-540-21902-1. Zbl 1159.11039.
Gaál, István (2002). Diophantine Equations and Power Integral Bases. Boston, MA: Birkhäuser Verlag. ISBN 978-0-8176-4271-6. Zbl 1016.11059.

This article is issued from Wikipedia - version of the Saturday, August 09, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.