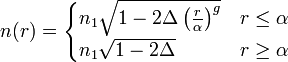Power-law index profile
For optical fibers, a power-law index profile is an index of refraction profile characterized by
where
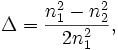
and 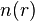 is the nominal refractive index as a function of distance from the fiber axis,
is the nominal refractive index as a function of distance from the fiber axis,  is the nominal refractive index on axis,
is the nominal refractive index on axis,  is the refractive index of the cladding, which is taken to be homogeneous (
is the refractive index of the cladding, which is taken to be homogeneous (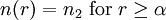 ),
),  is the core radius, and
is the core radius, and  is a parameter that defines the shape of the profile.
is a parameter that defines the shape of the profile.  is often used in place of
is often used in place of  . Hence, this is sometimes called an alpha profile.
. Hence, this is sometimes called an alpha profile.
For this class of profiles, multimode distortion is smallest when  takes a particular value depending on the material used. For most materials, this optimum value is approximately 2. In the limit of infinite
takes a particular value depending on the material used. For most materials, this optimum value is approximately 2. In the limit of infinite  , the profile becomes a step-index profile.
, the profile becomes a step-index profile.
See also
References
 This article incorporates public domain material from the General Services Administration document "Federal Standard 1037C".
This article incorporates public domain material from the General Services Administration document "Federal Standard 1037C".
This article is issued from Wikipedia - version of the Thursday, December 30, 2010. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.