Metallicity

The globular cluster M80. Stars in globular clusters are mainly older metal-poor members of Population II.

In astronomy and physical cosmology, the metallicity or Z is the fraction of mass of a star or other kind of astronomical object that is not in hydrogen (X) or helium (Y).[1][2] Most of the physical matter in the universe is in the form of hydrogen and helium, so astronomers use the word "metals" as a convenient short term for "all elements except hydrogen and helium".[3] This usage is distinct from the usual physical definition of a solid metal. The astronomical usage is claimed to be justified because in the high-temperature and pressure environment of a star, atoms do not undergo chemical reactions and effectively have no chemical properties, including that of being a metal as usually understood. For example, stars and nebulae with relatively high abundances of carbon, nitrogen, oxygen, and neon are called "metal-rich" in astrophysical terms, even though those elements are non-metals in chemistry.

The distinction between hydrogen and helium on the one hand and metals on the other is relevant because the primordial universe is believed to have contained virtually no metals, which were later synthesised within stars.

Metallicity within stars and other astronomical objects is an approximate estimation of their chemical abundances that change over time by the mechanisms of stellar evolution,[4] and therefore provide an indication of their age.[5] In cosmological terms, the universe is chemically evolving. According to the Big Bang Theory, the early universe first consisted of hydrogen and helium, with trace amounts of lithium and beryllium, but no heavier elements. Through the process of stellar evolution stars first generate energy by synthesising metals from hydrogen and helium by nuclear reactions, then disperse most of their mass by stellar winds or explode as supernovae, dispersing the new metals into the universe.[6] It is believed that older generations of stars generally have lower metallicities than those of younger generations,[7] having been formed in the metal-poor early universe.

Observed changes in the chemical abundances of different types of stars, based on the spectral peculiarities that were later attributed to metallicity, led astronomer Walter Baade in 1944 to propose the existence of two different populations of stars.[8] These became commonly known as Population I (metal-rich) and Population II (metal-poor) stars. A third stellar population was introduced in 1978, known as Population III stars.[9][10][11] These extremely metal-poor stars were theorised to have been the 'first-born' stars created in the universe.

Definition

Stellar composition, as determined by spectroscopy, is usually simply defined by the parameters X, Y and Z. Here X is the fractional percentage of hydrogen, Y is the fractional percentage of helium, and all the remaining chemical elements as the fractional percentage, Z. It is simply defined as;

X + Y + Z = 1.00

In most stars, nebulae and other astronomical sources, hydrogen and helium are the two dominant elements. The hydrogen mass fraction is generally expressed as X\equiv \frac{m_\mathrm{H}}{M} where M is the total mass of the system and m_\mathrm{H} the fractional mass of the hydrogen it contains. Similarly, the helium mass fraction is denoted as Y\equiv \frac{m_\mathrm{He}}{M}. The remainder of the elements are collectively referred to as 'metals', and the metallicity—the mass fraction of elements heavier than helium—can be calculated as

Z = \sum_{i>\mathrm{He}} \frac{m_i}{M} = 1 - X - Y.

For the Sun, these parameters are often assumed to have the following approximate values,[12] although recent research shows that lower values for 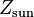Z_\mathrm{sun} might be more appropriate:[13][14]

Description Solar value
Hydrogen mass fraction X_\mathrm{sun} = 0.73
Helium mass fraction Y_\mathrm{sun} = 0.25
Metallicity Z_\mathrm{sun} = 0.02

The metallicity of many astronomical objects cannot be measured directly. Instead, proxies are used to obtain an indirect estimate. For example, an observer might measure the iron content of a galaxy (for example using the brightness of an iron emission line) directly, then compare that value with models to estimate the total metallicity.

Calculation

The overall stellar metallicity is often defined using the total iron-content of the star "[Fe/H]", since iron is not only the most abundant heavy element, but it is among the easiest to measure with spectral data in the visible spectrum. The abundance ratio is defined as the logarithm of the ratio of a star's iron abundance compared to that of the Sun and is expressed thus:

[\mathrm{Fe}/\mathrm{H}] = \log_{10}{\left(\frac{N_{\mathrm{Fe}}}{N_{\mathrm{H}}}\right)_\mathrm{star}} - \log_{10}{\left(\frac{N_{\mathrm{Fe}}}{N_{\mathrm{H}}}\right)_\mathrm{sun}}

where N_{\mathrm{Fe}} and N_{\mathrm{H}} are the number of iron and hydrogen atoms per unit of volume respectively. The unit often used for metallicity is the "dex" which is a (now-deprecated) contraction of 'decimal exponent'.[15] By this formulation, stars with a higher metallicity than the Sun have a positive logarithmic value, whereas those with a lower metallicity than the Sun have a negative value. The logarithm is based on powers of 10; stars with a value of +1 have ten times the metallicity of the Sun (101). Conversely, those with a value of −1 have one-tenth (10−1), while those with a value of −2 have a hundredth (10−2), and so on.[3] Young Population I stars have significantly higher iron-to-hydrogen ratios than older Population II stars. Primordial Population III stars are estimated to have a metallicity of less than −6.0, that is, less than a millionth of the abundance of iron in the Sun.

The same sort of notation is used to express differences in the individual elements from the solar proportion. For example, the notation "[O/Fe]" represents the difference in the logarithm of the star's oxygen abundance compared to that of the Sun and the logarithm of the star's iron abundance compared to the Sun:

[\mathrm{O}/\mathrm{Fe}] = \log_{10}{\left(\frac{N_{\mathrm{O}}}{N_{\mathrm{Fe}}}\right)_\mathrm{star}} - \log_{10}{\left(\frac{N_{\mathrm{O}}}{N_{\mathrm{Fe}}}\right)_\mathrm{sun}}
= \left[\log_{10}{\left(\frac{N_{\mathrm{O}}}{N_{\mathrm{H}}}\right)_\mathrm{star}} - \log_{10}{\left(\frac{N_{\mathrm{O}}}{N_{\mathrm{H}}}\right)_\mathrm{sun}}\right] - \left[\log_{10}{\left(\frac{N_{\mathrm{Fe}}}{N_{\mathrm{H}}}\right)_\mathrm{star}} - \log_{10}{\left(\frac{N_{\mathrm{Fe}}}{N_{\mathrm{H}}}\right)_\mathrm{sun}}\right].

The point of this notation is that if a mass of gas is diluted with pure hydrogen, then its [Fe/H] value will decrease (because there are fewer iron atoms per hydrogen atom after the dilution), but for all other elements X, the [X/Fe] ratios will remain unchanged. By contrast, if a mass of gas is polluted with some amount of pure oxygen, then its [Fe/H] will remain unchanged but its [O/Fe] ratio will increase. In general, a given stellar nucleosynthetic process alters the proportions of only a few elements or isotopes, so a star or gas sample with nonzero [X/Fe] values may be showing the signature of particular nuclear processes.

Relation between Z and [Fe/H]

These two ways of expressing the metallic content of a star are related through the equation:

\log_{10}\left(\frac{Z/X}{Z_\mathrm{sun}/X_\mathrm{sun}}\right) = [\mathrm{M}/\mathrm{H}]

where [M/H] is the star's total metal abundance (i.e. all elements heavier than helium) defined as a more general expression than the one for [Fe/H]:

[\mathrm{M}/\mathrm{H}] = \log_{10}{\left(\frac{N_{\mathrm{M}}}{N_{\mathrm{H}}}\right)_\mathrm{star}} - \log_{10}{\left(\frac{N_{\mathrm{M}}}{N_{\mathrm{H}}}\right)_\mathrm{sun}} .

The iron abundance and the total metal abundance are often assumed to be related through a constant A as:

[\mathrm{M}/\mathrm{H}] = A*[\mathrm{Fe}/\mathrm{H}]

where A assumes values between 0.9 and 1. Using the formulas presented above, the relation between Z and [Fe/H] can finally be written as:

\log_{10}\left(\frac{Z/X}{Z_\mathrm{sun}/X_\mathrm{sun}}\right) = A*[\mathrm{Fe}/\mathrm{H}].

See also

References

  1. ↑ D. Kunth & G. Östlin (2000). "The Most Metal-poor Galaxies" 10 (1). The Astronomy and Astrophysics Review. Retrieved 3 February 2015.
  2. ↑ W. Sutherland (26 March 2013). "The Galaxy. Chapter 4. Galactic Chemical Evolution" (PDF). Retrieved 13 January 2015.
  3. 1 2 John C. Martin. "What we learn from a star's metal content". New Analysis RR Lyrae Kinematics in the Solar Neighborhood. Retrieved September 7, 2005.
  4. ↑ McWilliam, Andrew (26 March 2013). "Abundance Ratios and galactic Chemical Evolution". Retrieved 13 January 2015.
  5. ↑ McWilliam, Andrew (1997-01-01). "Abundance Ratios and galactic Chemical Evolution : Age-Metallicity Relation". Retrieved 2015-01-13.
  6. ↑ F. Hoyle (1954). "On Nuclear Reactions Occurring in Very Hot Stars. I. the Synthesis of Elements from Carbon to Nickel.". Astrophysical Journal Supplement 1: 121–146. Bibcode:1954ApJS....1..121H. doi:10.1086/190005.
  7. ↑ McWilliam, Andrew (1997-01-01). "Abundance Ratios and galactic Chemical Evolution : Introduction". Retrieved 2015-01-13.
  8. ↑ W. Baade (1944). "The Resolution of Messier 32, NGC 205, and the Central Region of the Andromeda Nebula.". Astrophysical Journal 100: 121–146. Bibcode:1944ApJ...100..137B. doi:10.1086/144650.
  9. ↑ M.J. Rees (1978). "Origin of pregalactic microwave background". Nature 275: 35–37. Bibcode:1978Natur.275...35R. doi:10.1038/275035a0.
  10. ↑ S.D.M. White; M.J. Rees (1978). "Core condensation in heavy halos - A two-stage theory for galaxy formation and clustering". Monthly Notices Royal Astronomical Society 183: 341–358. Bibcode:1978MNRAS.183..341W. doi:10.1093/mnras/183.3.341.
  11. ↑ J.L. Puget; J. Heyvaerts (1980). "Population III stars and the shape of the cosmological black body radiation". Astronomy and Astrophysics 83: L10–L12. Bibcode:1980A&A....83L..10P.
  12. ↑ A. Unsöld; B. Baschek; R.C. Smith; C.A. Hein (1983). The New Cosmos. Springer New York. doi:10.1007/978-1-4757-1791-4. ISBN 978-0-387-90886-1.
  13. ↑ "The new solar abundances - Part I: the observations". Communications in Asteroseismology. January 2006. Retrieved 2013-06-25.
  14. ↑ "Solar Heavy-Element Abundance: Constraints from Frequency Separation Ratios of Low-Degree p-Modes". The Astrophysical Journal. November 2007. Retrieved 2013-06-30.
  15. ↑ R. Rowlett; et al. (July 2005). "How Many? A Dictionary of Units of Measurement". University of North Carolina. Retrieved 3 February 2015.

Sources

This article is issued from Wikipedia - version of the Sunday, January 31, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.