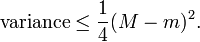Popoviciu's inequality on variances

In probability theory, Popoviciu's inequality, named after Tiberiu Popoviciu, is an upper bound on the variance of any bounded probability distribution. Let M and m be upper and lower bounds on the values of any random variable with a particular probability distribution. Then Popoviciu's inequality states:[1]

\text{variance} \le \frac14 (M - m)^2.

Sharma et al. have proved an improvement of the Popoviciu's inequality that says that:[2]

{\text {variance} + ( \frac \text {Third central moment} \text{2 variance} )^2} \le \frac14 (M - m)^2.

Equality holds precisely when half of the probability is concentrated at each of the two bounds.

Popoviciu's inequality is weaker than the Bhatia–Davis inequality.

References

  1. ↑ Popoviciu, T. (1935). "Sur les équations algébriques ayant toutes leurs racines réelles". Mathematica (Cluj) 9: 129–145.
  2. ↑ Sharma, R., Gupta, M., Kapoor, G. (2010). "Some better bound on variance with applications". Journal of mathematical inequalities 4: 355–363.


This article is issued from Wikipedia - version of the Monday, June 08, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.