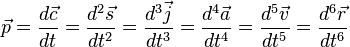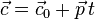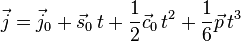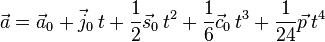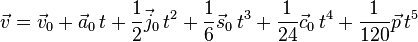Pop (physics)

In physics, pop is the sixth derivative of the position vector with respect to time, with the first, second, and third, fourth, and fifth derivatives being velocity, acceleration, jerk, snap, and crackle, respectively; in other words, the pop is the rate of change of the crackle with respect to time.[1][2] Pop is defined by any of the following equivalent expressions:

\vec p =\frac {d \vec c} {dt}=\frac {d^2 \vec s} {dt^2}=\frac {d^3 \vec j} {dt^3}=\frac {d^4 \vec a} {dt^4}=\frac {d^5 \vec v} {dt^5}=\frac {d^6 \vec r} {dt^6}

The following equations are used for constant pop:

\vec c = \vec c_0 + \vec p \,t
\vec s = \vec s_0 + \vec c_0 \,t + \frac{1}{2} \vec p \,t^2
\vec j = \vec j_0 + \vec s_0 \,t + \frac{1}{2} \vec c_0 \,t^2 + \frac{1}{6} \vec p \,t^3
\vec a = \vec a_0 + \vec j_0 \,t + \frac{1}{2} \vec s_0 \,t^2 + \frac{1}{6} \vec c_0 \,t^3 + \frac{1}{24} \vec p \,t^4
\vec v = \vec v_0 + \vec a_0 \,t + \frac{1}{2} \vec j_0 \,t^2 + \frac{1}{6} \vec s_0 \,t^3 + \frac{1}{24} \vec c_0 \,t^4 + \frac{1}{120} \vec p \,t^5
\vec r = \vec r_0 + \vec v_0 \,t + \frac{1}{2} \vec a_0 \,t^2 + \frac{1}{6} \vec j_0 \,t^3 + \frac{1}{24} \vec s_0 \,t^4 + \frac{1}{120} \vec c_0 \,t^5 + \frac{1}{720} \vec p \,t^6

where

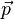\vec p : constant pop,
\vec c_0 : initial crackle,
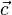\vec c : final crackle,
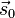\vec s_0 : initial jounce,
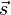\vec s : final jounce,
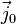\vec j_0 : initial jerk,
\vec j : final jerk,
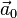\vec a_0 : initial acceleration,
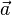\vec a : final acceleration,
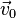\vec v_0 : initial velocity,
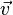\vec v : final velocity,
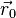\vec r_0 : initial position,
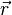\vec r : final position,
t : time between initial and final states.

The name "pop", along with "snap" (also referred to as jounce) and "crackle" are somewhat facetious terms for the fourth, fifth, and sixth derivatives of position, being a reference to Snap, Crackle, and Pop. Currently, there are no well-accepted designations for the derivatives of pop. Higher-order derivatives of position are not commonly useful. Thus, there has been no consensus among physicists on the proper names for derivatives above pop. Despite this, physicists have proposed other names such as "lock", "drop", "shot", and "put" for seventh, eighth, ninth and tenth derivatives.

Unit and dimension

The dimension of pop LT−6. In SI units, this is "metres per hexic second", "metres per second per second per second per second per second per second", m/s6, m · s−6, or 100 Gal per quartric second in CGS units. This pattern continues for higher order derivatives

References

  1. ↑ Thompson, Peter M. (5 May 2011). "Snap, Crackle, and Pop" (PDF). AIAA Info. Hawthorne, California: Systems Technology. p. 1. Retrieved 17 May 2015. The common names for the first three derivatives are velocity, acceleration, and jerk. The not so common names for the next three derivatives are snap, crackle, and pop.
  2. ↑ Visser, Matt (31 March 2004). "Jerk, snap and the cosmological equation of state" (PDF). Classical and Quantum Gravity (Victoria University of Wellington) 21 (11): 4. doi:10.1088/0264-9381/21/11/006. ISSN 0264-9381. Retrieved 17 May 2015. Snap [the fourth time derivative] is also sometimes called jounce. The fifth and sixth time derivatives are sometimes somewhat facetiously referred to as crackle and pop.
This article is issued from Wikipedia - version of the Wednesday, December 09, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.