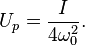Ponderomotive energy

In strong-field laser physics, ponderomotive energy is the cycle-averaged quiver energy of a free electron in an electromagnetic field.[1]

Equation

The ponderomotive energy is given by

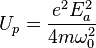U_p = {e^2 E_a^2 \over 4m \omega_0^2},

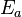where e is the electron charge, E_a is the linearly polarised electric field amplitude, 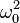\omega_0^2 is the laser carrier frequency and m is the electron mass.

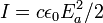In terms of the laser intensity I, using I=c\epsilon_0 E_a^2/2, it reads less simply:

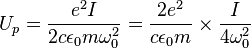U_p={e^2 I \over 2 c \epsilon_0 m \omega_0^2}={2e^2 \over c \epsilon_0 m} \times {I \over 4\omega_0^2},

where \epsilon_0 is the vacuum permittivity.

Atomic units

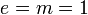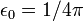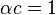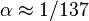In atomic units, e=m=1, \epsilon_0=1/4\pi, \alpha c=1 where \alpha \approx 1/137. If one uses the atomic unit of electric field,[2] then the ponderomotive energy is just

U_p = \frac{I}{4\omega_0^2}.

Derivation

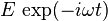The formula for the ponderomotive energy can be easily derived. A free electron of charge e interacts with an electric field E \, \exp(-i\omega t). The force on the electron is

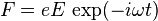F = eE \, \exp(-i\omega t).

The acceleration of the electron is

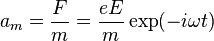a_{m} = {F \over m} = {e E \over m} \exp(-i\omega t).

Because the electron executes harmonic motion, the electron's position is

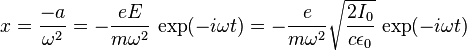x = {-a \over \omega^2}= -\frac{eE}{m\omega^2} \, \exp(-i\omega t) = -\frac{e}{m\omega^2} \sqrt{\frac{2I_0}{c\epsilon_0}} \, \exp(-i\omega t).

For a particle experiencing harmonic motion, the time-averaged energy is

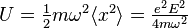U = \textstyle{\frac{1}{2}}m\omega^2 \langle x^2\rangle = {e^2 E^2 \over 4 m \omega^2}.

In laser physics, this is called the ponderomotive energy U_p.

See also

References and notes

  1. ↑ Highly Excited Atoms. By J. P. Connerade. p. 339
  2. ↑ CODATA Value: atomic unit of electric field
This article is issued from Wikipedia - version of the Friday, December 18, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.