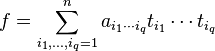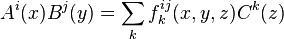Ring of polynomial functions

In mathematics, the ring of polynomial functions on a vector space V over an infinite field k gives a coordinate-free analog of a polynomial ring. It is denoted by k[V]. If V has finite dimension and is viewed as an algebraic variety, then k[V] is precisely the coordinate ring of V.

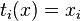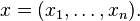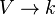The explicit definition of the ring can be given as follows. If k[t_1, \dots, t_n] is a polynomial ring, then we can view t_i as coordinate functions on k^n; i.e., t_i(x) = x_i when x = (x_1, \dots, x_n). This suggests the following: given a vector space V, let k[V] be the subring generated by the dual space V^* of the ring of all functions V \to k. If we fix a basis for V and write t_i for its dual basis, then k[V] consists of polynomials in t_i; it is a polynomial ring.

In applications, one also defines k[V] when V is defined over some subfield of k (e.g., k is the complex field and V is a real vector space.) The same definition still applies.

Symmetric multilinear maps

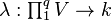Let S^q(V) denote the vector space of multilinear functionals \textstyle \lambda: \prod_1^q V \to k that are symmetric; 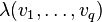\lambda(v_1, \dots, v_q) is the same for all permutations of v_i's.

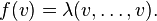Any λ in S^q(V) gives rise to a homogeneous polynomial function f of degree q: let f(v) = \lambda(v, \dots, v). To see that f is a polynomial function, choose a basis 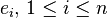e_i, \, 1 \le i \le n of V and t_i its dual. Then

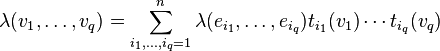\lambda(v_1, \dots, v_q) = \sum_{i_1, \dots, i_q = 1}^n \lambda(e_{i_1}, \dots, e_{i_q}) t_{i_1}(v_1) \cdots t_{i_q}(v_q).

Thus, there is a well-defined linear map:

\phi: S^q(V) \to k[V]_q, \, \phi(\lambda)(v) = \lambda(v, \cdots, v).

It is an isomorphism:[1] choosing a basis as before, any homogeneous polynomial function f of degree q can be written as:

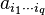f = \sum_{i_1, \dots, i_q = 1}^n a_{i_1 \cdots i_q} t_{i_1} \cdots t_{i_q}

where a_{i_1 \cdots i_q} are symmetric in 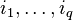i_1, \dots, i_q. Let

\psi(f)(v_1, \dots, v_q) = \sum_{i_1, \cdots, i_q = 1}^n a_{i_1 \cdots i_q} t_{i_1}(v_1) \cdots t_{i_q}(v_q).

Then ψ is the inverse of φ. (Note: φ is still independent of a choice of basis; so ψ is also independent of a basis.)

Example: A bilinear functional gives rise to a quadratic form in a unique way and any quadratic form arises in this way.

Operator product algebra

When the polynomials are valued not over a field k, but instead are valued over some algebra, then one may define additional structure. Thus, for example, one may consider the ring of functions over GL(n,m), instead of for k = GL(1,m). In this case, one may impose an additional axiom.

The operator product algebra is an associative algebra of the form

A^i(x)B^j(y) = \sum_k f^{ij}_k (x,y,z) C^k(z)

The structure constants 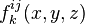f^{ij}_k (x,y,z) are required to be single-valued functions, rather than sections of some vector bundle. The fields (or operators) 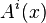A^i(x) are required to span the ring of functions. In practical calculations, it is usually required that the sums be analytic within some radius of convergence; typically with a radius of convergence of 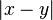|x-y|. Thus, the ring of functions can be taken to be the ring of polynomial functions.

The above can be considered to be an additional requirement imposed on the ring; it is sometimes called the bootstrap. In physics, a special case of the operator product algebra is known as the operator product expansion.

See also

Notes

  1. ↑ There is also a more abstract way to see this: to give a multilinear functional on the product of q copies of V is the same as to give a linear functional on the q-th tensor power of V. The requirement that the multilinear functional to be symmetric translates to the one that the linear functional on the tensor power factors through the q-th symmetric power of V, which is isomorphic to k[V]q.

References

This article is issued from Wikipedia - version of the Friday, September 18, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.