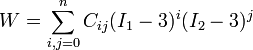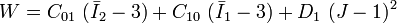Polynomial (hyperelastic model)

The polynomial hyperelastic material model [1] is a phenomenological model of rubber elasticity. In this model, the strain energy density function is of the form of a polynomial in the two invariants I_1,I_2 of the left Cauchy-Green deformation tensor.

The strain energy density function for the polynomial model is [1]

W = \sum_{i,j=0}^n C_{ij} (I_1 - 3)^i (I_2 - 3)^j

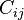where C_{ij} are material constants and C_{00}=0.

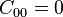For compressible materials, a dependence of volume is added

W = \sum_{i,j=0}^n C_{ij} (\bar{I}_1 - 3)^i (\bar{I}_2 - 3)^j + \sum_{k=1}^m D_{k}(J-1)^{2k}

where

\begin{align} \bar{I}_1 & = J^{-2/3}~I_1 ~;~~ I_1 = \lambda_1^2 + \lambda_2 ^2+ \lambda_3 ^2 ~;~~ J = \det(\boldsymbol{F}) \\ \bar{I}_2 & = J^{-4/3}~I_2 ~;~~ I_2 = \lambda_1^2 \lambda_2^2 + \lambda_2^2 \lambda_3^2 + \lambda_3^2 \lambda_1^2 \end{align}

In the limit where 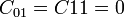C_{01}=C{11}=0, the polynomial model reduces to the Neo-Hookean solid model. For a compressible Mooney-Rivlin material 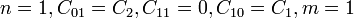n = 1, C_{01} = C_2, C_{11} = 0, C_{10} = C_1, m=1 and we have

W = C_{01}~(\bar{I}_2 - 3) + C_{10}~(\bar{I}_1 - 3) + D_1~(J-1)^2

References

  1. ↑ 1.0 1.1 Rivlin, R. S. and Saunders, D. W., 1951, Large elastic deformations of isotropic materials VII. Experiments on the deformation of rubber. Phi. Trans. Royal Soc. London Series A, 243(865), pp. 251-288.

See also

This article is issued from Wikipedia - version of the Tuesday, October 22, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.