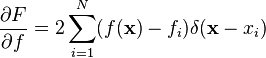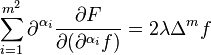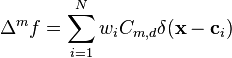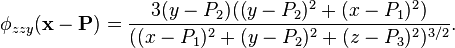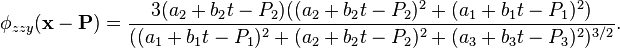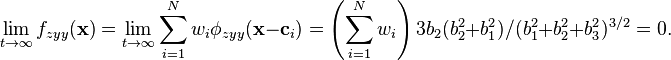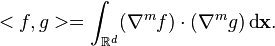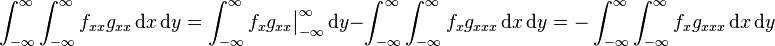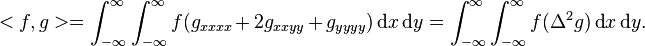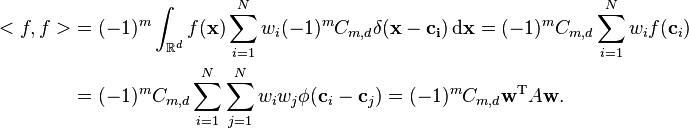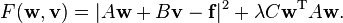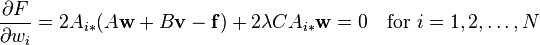Polyharmonic spline
Polyharmonic splines are used for function approximation and data interpolation. They are very useful for interpolating and fitting scattered data in many dimensions. A special case is the thin plate spline.[1][2]
Definition
A polyharmonic spline is a linear combination of polyharmonic radial basis functions (RBFs) (denoted by  ) plus an optional linear term:
) plus an optional linear term:
-
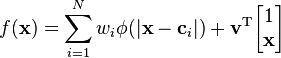
(1)
where

-
![\mathbf{x} = [x_1, x_2, \cdots, x_{d}]^{\textrm{T}}](../I/m/4a11625839090aa3b4199b6a8ebf2e91.png) is a real-valued vector of
is a real-valued vector of 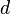 independent variables,
independent variables, -
![\mathbf{c}_i = [c_{i,1}, c_{i,2}, \cdots, c_{i,d}]^{\textrm{T}}](../I/m/7871ec09ff6c825a4bdf80bb9c981e1b.png) are
are  vectors of the same size as
vectors of the same size as 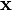 (often called centers) that the curve or surface must interpolate
(often called centers) that the curve or surface must interpolate -
![\mathbf{w} = [w_1, w_2, \cdots, w_N]^{\textrm{T}}](../I/m/50e7b1a5ca1d2a18c64dcd009a31083c.png) are the
are the  weights of the RBFs.
weights of the RBFs. -
![\mathbf{v} = [v_1, v_2, \cdots, v_{d+1}]^{\textrm{T}}](../I/m/881c93425abf49c270279ebb59715467.png) are the
are the  weights of the polynomial.
weights of the polynomial. - The linear polynomial with the weighting factors
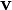 improves the interpolation close to the "boundary" and especially the extrapolation "outside" of the centers
improves the interpolation close to the "boundary" and especially the extrapolation "outside" of the centers 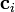 . If this is not desired, this term can also be removed (see also figure below).
. If this is not desired, this term can also be removed (see also figure below).
The polyharmonic RBFs are of the form:
Other values of the exponent  are not useful (such as
are not useful (such as 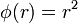 ), because a solution of the interpolation problem might not exist. To avoid problems at
), because a solution of the interpolation problem might not exist. To avoid problems at 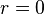 (since
(since 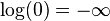 ), the polyharmonic RBFs with the natural logarithm might be implemented as:
), the polyharmonic RBFs with the natural logarithm might be implemented as:
The weights  and
and  are determined such that the function interpolates
are determined such that the function interpolates  given points
given points 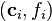 (for
(for 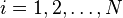 ) and fulfills the
) and fulfills the  orthogonality conditions:
orthogonality conditions:
All together, these constraints are equivalent to the following symmetric linear system of equations:
-

(2)
where
Under very mild conditions (essentially, that at least  points are not in a subspace; e.g. for
points are not in a subspace; e.g. for 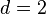 that at least 3 points are not on a straight line), the matrix of the linear system of equations is nonsingular and therefore a unique solution of the equation system exists. The computed weights allow evaluation of the spline for any
that at least 3 points are not on a straight line), the matrix of the linear system of equations is nonsingular and therefore a unique solution of the equation system exists. The computed weights allow evaluation of the spline for any  using equation (1).
using equation (1).
Many practical details to implement and use polyharmonic splines are given in Fasshauer.[3] In Iske[4] polyharmonic splines are treated as special cases of other multiresolution methods in scattered data modelling.
Reason for the name "polyharmonic"
A polyharmonic equation is a partial differential equation of the form 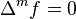 for any natural number
for any natural number  . For example, the biharmonic equation is
. For example, the biharmonic equation is 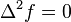 and the triharmonic equation is
and the triharmonic equation is 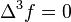 . All the polyharmonic radial basis functions are solutions of a polyharmonic equation (or more accurately, a modified polyharmonic equation with a Dirac delta function on the right hand side instead of 0). For example, the thin plate radial basis function is a solution of the modified 2-dimensional biharmonic equation. [5] Applying the 2D Laplace operator (
. All the polyharmonic radial basis functions are solutions of a polyharmonic equation (or more accurately, a modified polyharmonic equation with a Dirac delta function on the right hand side instead of 0). For example, the thin plate radial basis function is a solution of the modified 2-dimensional biharmonic equation. [5] Applying the 2D Laplace operator (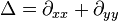 ) to the thin plate radial basis function
) to the thin plate radial basis function 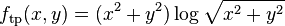 either by hand or using a computer algebra system shows that
either by hand or using a computer algebra system shows that 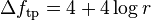 . Applying the Laplace operator to
. Applying the Laplace operator to 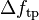 (this is
(this is 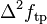 ) yields 0. But 0 is not exactly correct. To see this, replace
) yields 0. But 0 is not exactly correct. To see this, replace 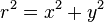 with
with 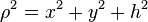 (where
(where  is some small number tending to 0). The Laplace operator applied to
is some small number tending to 0). The Laplace operator applied to 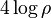 yields
yields 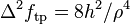 . For
. For 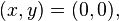 the right hand side of this equation approaches infinity as
the right hand side of this equation approaches infinity as  approaches 0. For any other
approaches 0. For any other 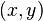 , the right hand side approaches 0 as
, the right hand side approaches 0 as  approaches 0. This indicates that the right hand side is a Dirac delta function. A computer algebra system will show that
approaches 0. This indicates that the right hand side is a Dirac delta function. A computer algebra system will show that
So the thin plate radial basis function is a solution of the equation 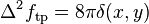 .
.
Applying the 3D Laplacian (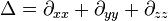 ) to the biharmonic RBF
) to the biharmonic RBF 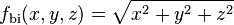 yields
yields 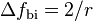 and applying the 3D
and applying the 3D  operator to the triharmonic RBF
operator to the triharmonic RBF 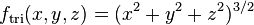 yields
yields 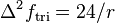 . Letting
. Letting 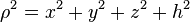 and computing
and computing 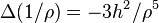 again indicates that the right hand side of the PDEs for the biharmonic and triharmonic RBFs are Dirac delta functions. Since
again indicates that the right hand side of the PDEs for the biharmonic and triharmonic RBFs are Dirac delta functions. Since
the exact PDEs satisfied by the biharmonic and triharmonic RBFs are 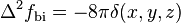 and
and 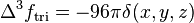 .
.
Polyharmonic smoothing splines
Polyharmonic splines minimize
-
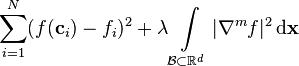
(3)
where  is some box in
is some box in  containing a neighborhood of all the centers,
containing a neighborhood of all the centers,  is some positive constant, and
is some positive constant, and 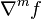 is the vector of all
is the vector of all  th order partial derivatives of
th order partial derivatives of  For example, in 2D
For example, in 2D 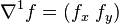 and
and 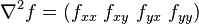 and in 3D
and in 3D 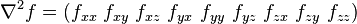 . In 2D
. In 2D 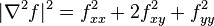 , making the integral the simplified thin plate energy functional.
, making the integral the simplified thin plate energy functional.
To show that polyharmonic splines minimize equation (3), the fitting term must be transformed into an integral using the definition of the Dirac delta function:
So equation (3) can be written as the functional
where  is a multi-index that ranges over all partial derivatives of order
is a multi-index that ranges over all partial derivatives of order  for
for  . In order to apply the Euler-Lagrange equation for a single function of multiple variables and higher order derivatives, the quantities
. In order to apply the Euler-Lagrange equation for a single function of multiple variables and higher order derivatives, the quantities
and
are needed. Inserting these quantities into the E-L equation shows that
-
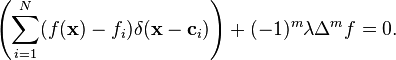
(4)
Let  be a polyharmonic spline as defined by equation (1). The following calculations will show that
be a polyharmonic spline as defined by equation (1). The following calculations will show that  satisfies (4). Applying the
satisfies (4). Applying the 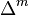 operator to equation (1) yields
operator to equation (1) yields
where 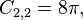
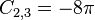 , and
, and 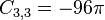 . So
. So
-
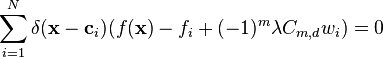
(5)
is equivalent to (4). Setting
-
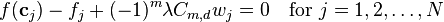
(6)
(which implies interpolation if 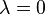 ) solves equation (5) and hence solves (4). Combining the definition of
) solves equation (5) and hence solves (4). Combining the definition of  in equation (1) with equation (6) results in almost the same linear system as equation (2) except that the matrix
in equation (1) with equation (6) results in almost the same linear system as equation (2) except that the matrix  is replaced with
is replaced with 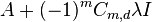 where
where  is the
is the  identity matrix. For example, for the 3D triharmonic RBFs,
identity matrix. For example, for the 3D triharmonic RBFs,  is replaced with
is replaced with 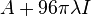 .
.
Explanation of additional constraints
In (2), the bottom half of the system of equations (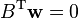 ) is given without explanation. The explanation first requires deriving a simplified form of
) is given without explanation. The explanation first requires deriving a simplified form of 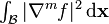 when
when  is all of
is all of 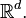
First, require that 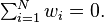 This ensures that all derivatives of order
This ensures that all derivatives of order  and higher of
and higher of 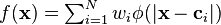 vanish at infinity. For example, let
vanish at infinity. For example, let 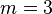 and
and 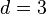 and
and  be the triharmonic RBF. Then
be the triharmonic RBF. Then 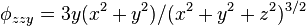 (considering
(considering  as a mapping from
as a mapping from 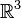 to
to 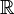 ). For a given center
). For a given center 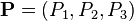 ,
,
On a line 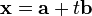 for arbitrary point
for arbitrary point  and unit vector
and unit vector 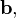
Dividing both numerator and denominator of this by 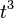 shows that
shows that 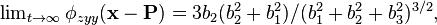 a quantity independent of the center
a quantity independent of the center 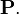 So on the given line,
So on the given line,
It is not quite enough to require that 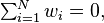 because in what follows it is necessary for
because in what follows it is necessary for 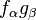 to vanish at infinity, where
to vanish at infinity, where  and
and 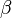 are multi-indices such that
are multi-indices such that 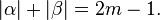 For triharmonic
For triharmonic 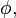
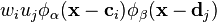 (where
(where 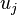 and
and 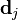 are the weights and centers of
are the weights and centers of  ) is always a sum of total degree 5 polynomials in
) is always a sum of total degree 5 polynomials in 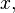
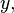 and
and 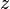 divided by the square root of a total degree 8 polynomial. Consider the behavior of these terms on the line
divided by the square root of a total degree 8 polynomial. Consider the behavior of these terms on the line 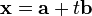 as
as  approaches infinity. The numerator is a degree 5 polynomial in
approaches infinity. The numerator is a degree 5 polynomial in 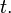 Dividing numerator and denominator by
Dividing numerator and denominator by 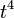 leaves the degree 4 and 5 terms in the numerator and a function of
leaves the degree 4 and 5 terms in the numerator and a function of  only in the denominator. A degree 5 term divided by
only in the denominator. A degree 5 term divided by 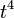 is a product of five
is a product of five  coordinates and
coordinates and 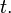 The
The 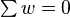 (and
(and 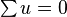 ) constraint makes this vanish everywhere on the line. A degree 4 term divided by
) constraint makes this vanish everywhere on the line. A degree 4 term divided by 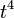 is either a product of four
is either a product of four  coordinates and an
coordinates and an  coordinate or a product of four
coordinate or a product of four  coordinates and a single
coordinates and a single 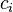 or
or  coordinate. The
coordinate. The 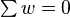 constraint makes the first type of term vanish everywhere on the line. The additional constraints
constraint makes the first type of term vanish everywhere on the line. The additional constraints 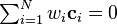 will make the second type of term vanish.
will make the second type of term vanish.
Now define the inner product of two functions 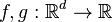 defined as a linear combination of polyharmonic RBFs
defined as a linear combination of polyharmonic RBFs 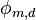 with weights summing to 0 as
with weights summing to 0 as
Integration by parts shows that
-
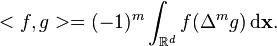
(7)
For example, let 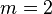 and
and 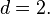 Then
Then
-
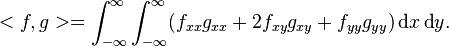
(8)
Integrating the first term of this by parts once yields
since 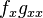 vanishes at infinity. Integrating by parts again results in
vanishes at infinity. Integrating by parts again results in 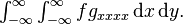
So integrating by parts twice for each term of (8) yields
Since 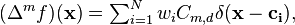 (7) shows that
(7) shows that
So if 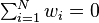 and
and 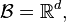
-
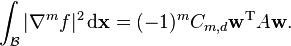
(9)
Now the origin of the constraints 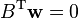 can be explained.
Here
can be explained.
Here  is a generalization of the
is a generalization of the  defined above to possibly include monomials up to degree
defined above to possibly include monomials up to degree 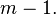 In other words,
In other words,
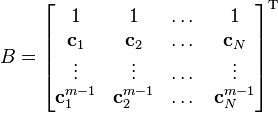
where 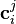 is a column vector of all degree
is a column vector of all degree 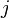 monomials of the coordinates of
monomials of the coordinates of 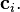 The top half of (2) is equivalent to
The top half of (2) is equivalent to
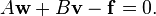 So to obtain a smoothing spline, one should minimize the scalar field
So to obtain a smoothing spline, one should minimize the scalar field
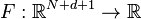 defined by
defined by
The equations
and
(where 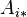 denotes row
denotes row  of
of  ) are equivalent to the two systems of linear equations
) are equivalent to the two systems of linear equations
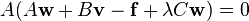 and
and
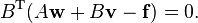 Since
Since  is invertible, the first system is equivalent to
is invertible, the first system is equivalent to
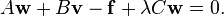 So the first system implies the second system is equivalent to
So the first system implies the second system is equivalent to 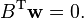 Just as in the previous smoothing spline coefficient derivation, the top half of (2) becomes
Just as in the previous smoothing spline coefficient derivation, the top half of (2) becomes
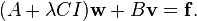
This derivation of the polyharmonic smoothing spline equation system did not assume the constraints necessary to guarantee that 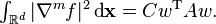 But the constraints necessary to guarantee this,
But the constraints necessary to guarantee this, 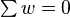 and
and 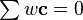 , are a subset of
, are a subset of 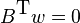 which is true for the critical point
which is true for the critical point  of
of 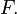 So
So 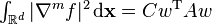 is true for the
is true for the  formed from the solution of the polyharmonic smoothing spline equation. Because the integral is positive for all
formed from the solution of the polyharmonic smoothing spline equation. Because the integral is positive for all 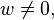 the linear transfomation resulting from the restriction of the domain of linear transformation
the linear transfomation resulting from the restriction of the domain of linear transformation  to
to  such that
such that 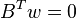 must be positive definite. This fact enables transforming the polyharmonic smoothing spline equation system to a symmetric positive definite system of equations that can be solved twice as fast using the Cholesky decomposition.[5]
must be positive definite. This fact enables transforming the polyharmonic smoothing spline equation system to a symmetric positive definite system of equations that can be solved twice as fast using the Cholesky decomposition.[5]
Examples
The next figure shows the interpolation through four points (marked by "circles") using different types of polyharmonic splines. The "curvature" of the interpolated curves grows with the order of the spline and the extrapolation at the left boundary (x < 0) is reasonable. The figure also includes the radial basis functions phi = exp(-r2) which gives a good interpolation as well. Finally, the figure includes also the non-polyharmonic spline phi = r2 to demonstrate, that this radial basis function is not able to pass through the predefined points (the linear equation has no solution and is solved in a least squares sense).

The next figure shows the same interpolation as in the first figure, with the only exception that the points to be interpolated are scaled by a factor of 100 (and the case phi = r2 is no longer included). Since phi = (scale*r)k = (scalek)*rk, the factor (scalek) can be extracted from matrix A of the linear equation system and therefore the solution is not influenced by the scaling. This is different for the logarithmic form of the spline, although the scaling has not much influence. This analysis is reflected in the figure, where the interpolation shows not much differences. Note, for other radial basis functions, such as phi = exp(-k*r2) with k=1, the interpolation is no longer reasonable and it would be necessary to adapt k.

The next figure shows the same interpolation as in the first figure, with the only exception that the polynomial term of the function is not taken into account (and the case phi = r2 is no longer included). As can be seen from the figure, the extrapolation for x < 0 is no longer as "natural" as in the first figure for some of the basis functions. This indicates, that the polynomial term is useful if extrapolation occurs.

Discussion
The main advantage of polyharmonic spline interpolation is that usually very good interpolation results are obtained for scattered data without performing any "tuning", so automatic interpolation is feasible. This is not the case for other radial basis functions. For example, the Gaussian function 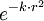 needs to be tuned, so that
needs to be tuned, so that  is selected according to the underlying grid of the independent variables. If this grid is non-uniform, a proper selection of
is selected according to the underlying grid of the independent variables. If this grid is non-uniform, a proper selection of  to achieve a good interpolation result is difficult or impossible.
to achieve a good interpolation result is difficult or impossible.
Main disadvantages are:
- To determine the weights, a linear system of equations must be solved, which is non-sparse. The solution of a non-sparse linear system becomes no longer practical if the dimension n is larger as about 1000 (since the storage requirements are O(n2) and the number of operations to solve the linear system is O(n3). For example n=10000 requires about 100 Mbyte of storage and 1000 Gflops of operations).
- To perform the interpolation of M data points requires operations in the order of O(M*N). In many applications, like image processing, M is much larger than N, and if both numbers are large, this is no longer practical.
Recently, methods have been developed to overcome the aforementioned difficulties. For example Beatson et al.[6] present a method to interpolate polyharmonic splines at one point in 3 dimensions in O(log(N)) instead of O(N).
See also
- Inverse distance weighting
- Radial basis function
- Subdivision surface (emerging alternative to spline-based surfaces)
- Spline
References
- ↑ R.L. Harder and R.N. Desmarais: Interpolation using surface splines. Journal of Aircraft, 1972, Issue 2, pp. 189-191
- ↑ J. Duchon: Splines minimizing rotation-invariant semi-norms in Sobolev spaces. Constructive Theory of Functions of Several Variables, W. Schempp and K. Zeller (eds), Springer, Berlin, pp.85-100
- ↑ G.F. Fasshauer G.F.: Meshfree Approximation Methods with MATLAB. World Scientific Publishing Company, 2007, ISPN-10: 9812706348
- ↑ A. Iske: Multiresolution Methods in Scattered Data Modelling, Lecture Notes in Computational Science and Engineering, 2004, Vol. 37, ISBN 3-540-20479-2, Springer-Verlag, Heidelberg.
- 1 2 Powell, M. J. D. (1993). "Some algorithms for thin plate spline interpolation to functions of two variables" (PDF). Cambridge University Dept. of Applied Mathematics and Theoretical Physics technical report. Retrieved January 7, 2016.
- ↑ R.K. Beatson, M.J.D. Powell, and A.M. Tan A.M.: Fast evaluation of polyharmonic splines in three dimensions. IMA Journal of Numerical Analysis, 2007, 27, pp. 427-450.
![\begin{matrix}
\phi(r) = \begin{cases}
r^k & \mbox{with } k=1,3,5,\dots, \\
r^k \ln(r) & \mbox{with } k=2,4,6,\dots
\end{cases} \\[5mm]
r = |\mathbf{x} - \mathbf{c}_i|
= \sqrt{ (\mathbf{x} - \mathbf{c}_i)^T \, (\mathbf{x} - \mathbf{c}_i) }.
\end{matrix}](../I/m/eafe4d7dd5e73c3957a2e8732c6d296a.png)
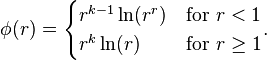
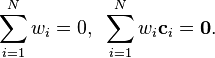
![A_{i,j} = \phi(|\mathbf{c}_i - \mathbf{c}_j|), \quad
B =
\begin{bmatrix}
1 & 1 & \cdots & 1 \\
\mathbf{c}_1 & \mathbf{c}_2 & \cdots & \mathbf{c}_{N}
\end{bmatrix}^{\textrm{T}}, \quad
\mathbf{f} = [f_1, f_2, \cdots, f_N]^{\textrm{T}}](../I/m/93de640788f30b5116253482d52db3f5.png)
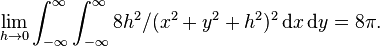
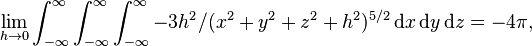
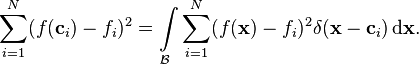
![J[f] = \int\limits_{\mathcal{B}} F(\mathbf{x},f, \partial^{\alpha_1}f, \partial^{\alpha_2}f, \dots \partial^{\alpha_n}f ) \operatorname{d}\!\mathbf{x} = \int\limits_{\mathcal{B}} \left[ \sum_{i=1}^N (f(\mathbf{x}) - f_i)^2 \delta(\mathbf{x} - \mathbf{c}_i) + \lambda |\nabla^m f|^2 \right] \operatorname{d}\!\mathbf{x}.](../I/m/761e1266293c4199db8220970994d1c5.png)