Polygon partition

A partition of a polygon is a set of primitive units (e.g. squares), which do not overlap and whose union equals the polygon. A polygon partition problem is a problem of finding a partition which is minimal in some sense, for example: a partition with a smallest number of units or with units of smallest total side-length.

Polygon partitioning is an important class of problems in computational geometry. There are many different polygon partition problems, depending on the type of polygon being partitioned and on the types of units allowed in the partition.

The term polygon decomposition is often used as a general term that includes both covering and partitioning.^[1]

Applications

Polygon decomposition is applied in several areas:^[1]

Pattern recognition techniques extract information from an object in order to describe, identify or classify it. An established strategy for recognising a general polygonal object is to decompose it into simpler components, then identify the components and their interrelationships and use this information to determine the shape of the object.
In VLSI artwork data processing, layouts are represented as polygons, and one approach to preparation for electron-beam lithography is to decompose these polygon regions into fundamental figures. Polygon decomposition is also used in the process of dividing the routing region into channels.
In computational geometry, algorithms for problems on general polygons are often more complex than those for restricted types of polygons such as convex or star-shaped. The point inclusion problem is one example. A strategy for solving some of these types of problems on general polygons is to decompose the polygon into simple component parts, solve the problem on each component using a specialized algorithm, and then combine the partial solutions.
Other applications include data compression, database systems, image processing and computer graphics.

Partitioning a polygon to triangles

Main articles: Polygon triangulation and Minimum-weight triangulation

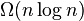The most well-studied polygon partition problem is partitioning to a smallest number of triangles, also called triangulation. For a hole-free polygon with $n$ vertices, a triangulation can be calculated in time $\Theta(n)$ . For a polygon with holes, there is a lower bound of $\Omega(n \log n)$ .

A related problem is partitioning to triangles with a minimal total edge length, also called Minimum-weight triangulation.

Partitioning a polygon to pseudo-triangles

Main article: Pseudotriangle § Pseudotriangulations

The same two variants of the problem were studied for the case in which the pieces should be pseudotriangles - polygons that like triangles have exactly three convex vertices. The variants are: partitioning to a smallest number of pseodutriangles, and partitioning to pseudotriangles with a minimal total edge length.

Partitioning a rectilinear polygon to rectangles

A special sub-family of polygon partition problems arises when the large polygon is a rectilinear polygon (also called: orthogonal polygon). In this case, the most important component shape to consider is the rectangle.^[1]

Rectangular partitions have many applications. In VLSI design, it is necessary to decompose masks into the simpler shapes available in lithographic pattern generators, and similar mask decomposition problems also arise in DNA microarray design. Rectangular partitions can simplify convolution operations in image processing and can be used to compress bitmap images. Closely related matrix decomposition problems have been applied to radiation therapy planning, and rectangular partitions have also been used to design robot self-assembly sequences.^[2]

Several polynomial-time algorithms for this problem are known; see ^[1]^:10-13 and ^[2]^:3-5 for a review.

The problem of partitioning a rectilinear polygon to a smallest number of squares (in contrast to arbitrary rectangles) is NP-hard.^[3]

Partition a polygon to trapezoids

in VLSI artwork processing systems, it is often required to partition a polygonal region into the minimum number of trapezoids, with two horizontal sides. A triangle with a horizontal side is considered to be a trapezoid with two horizontal sides one of which is degenerate. For a hole-free polygon with $n$ sides, a smallest such partition can be found in time $O(n^3)$ .^[4]

If the number of trapezoids need not be minimal a trapezoidation can be found in time $O(n)$ , as a by-product of a polygon triangulation algorithm.^[5]

If the polygon does contain holes, the problem is NP-complete, but a 3-approximation can be found in time $O(n\log n)$ .^[4]

Partition a polygon to convex quadrilaterals

A quadrilateralization or a quadrangulation is a partition into quadrilaterals.

A recurring characteristic of quadrangulation problems is whether they Steiner point are allowed, i.e, whether the algorithm is allowed to add points which are not vertices of the polygon. Allowing Steiner points may enable smaller divisios, but then it is much more difficult to guarantee that the divisions found by an algorithms have minimum size.

There are linear-time algorithms for quadrangulations of hole-free polygons with Steiner points, but they are not guaranteed to find a smallest partition.^[6]^[7]

Partition a polygon to m-gons

A generalization of previous problems is the problem of partitioning to polygons that have exactly m sides, or at most m sides. Here the goal is to minimize the total edge length. This problem can be solved in time polynomial in n and m.^[8]^[9]

More general component shapes

More general shapes of pieces have been studied, including: arbitrary convex polygons, spiral shapes, star polygons and monotone polygons. See ^[1] for a survey.

References

{{Cite book|doi=10.1016/B978-044482537-7/50012-7|chapter=Polygon Decomposition|title=Handbook of Computational Geometry|pages=491|year=2000|last1=Mark Keil|first1=J.|isbn=9780444825377}}</ref>

^[2] ^[10] ^[4]; -webkit-column-width: ^[1] ^[2] ^[10] ^[4]; column-width: ^[1] ^[2] ^[10] ^[4]; list-style-type: decimal;">

1 2 3 4 5 6 7 Mark Keil, J. (2000). "Polygon Decomposition". Handbook of Computational Geometry. p. 491. doi:10.1016/B978-044482537-7/50012-7. ISBN 9780444825377.
1 2 3 4 5 Eppstein, David (2010). "Graph-Theoretic Solutions to Computational Geometry Problems". Graph-Theoretic Concepts in Computer Science. Lecture Notes in Computer Science 5911. p. 1. doi:10.1007/978-3-642-11409-0_1. ISBN 978-3-642-11408-3.
↑ Realz Slaw. "Tiling an orthogonal polygon with squares". CS stack exchange. Retrieved 19 October 2015.
1 2 3 4 5 Asano, Takao; Asano, Tetsuo; Imai, Hiroshi (1986). "Partitioning a polygonal region into trapezoids". Journal of the ACM 33 (2): 290. doi:10.1145/5383.5387.
↑ Chazelle, Bernard (2007). "Triangulating a simple polygon in linear time". Discrete & Computational Geometry 6 (3): 485. doi:10.1007/bf02574703.
↑ H. Everett, W. Lenhart, M. Overmars, T. Shermer, J. Urrutia. (1992). "Strictly convex quadrilateralizations of polygons". Proc. 4th Canad. Conf. Comput. Geom. pp. 77–83. |access-date= requires |url= (help)
↑ Ramaswami, Suneeta; Ramos, Pedro; Toussaint, Godfried (1998). "Converting triangulations to quadrangulations". Computational Geometry 9 (4): 257. doi:10.1016/s0925-7721(97)00019-9.
↑ Lingas, Andrzej; Levcopoulos, Christos; Sack, Jörg (1987). "Algorithms for minimum length partitions of polygons". BIT 27 (4): 474. doi:10.1007/bf01937272.
↑ Levcopoulos, Christos; Lingas, Andrzej; Sack, Jörg-R. (1989). "Heuristics for optimum binary search trees and minimum weight triangulation problems". Theoretical Computer Science 66 (2): 181. doi:10.1016/0304-3975(89)90134-5.
1 2 3 Lingas, Andrzej (1982). "The power of non-rectilinear holes". Automata, Languages and Programming. Lecture Notes in Computer Science 140. p. 369. doi:10.1007/bfb0012784. ISBN 3-540-11576-5.

This article is issued from Wikipedia - version of the Friday, February 12, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.