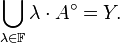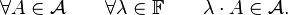Polar topology
In functional analysis and related areas of mathematics a polar topology, topology of  -convergence or topology of uniform convergence on the sets of
-convergence or topology of uniform convergence on the sets of  is a method to define locally convex topologies on the vector spaces of a dual pair.
is a method to define locally convex topologies on the vector spaces of a dual pair.
Definitions
Let  be a dual pair of vector spaces
be a dual pair of vector spaces  and
and 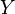 over the field
over the field 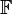 , either the real or complex numbers.
, either the real or complex numbers.
A set 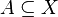 is said to be bounded in
is said to be bounded in  with respect to
with respect to 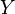 , if for each element
, if for each element  the set of values
the set of values 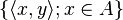 is bounded:
is bounded:
This condition is equivalent to the requirement that the polar  of the set
of the set  in
in 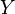
is an absorbent set in 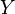 , i.e.
, i.e.
Let now  be a family of bounded sets in
be a family of bounded sets in  (with respect to
(with respect to 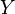 ) with the following properties:
) with the following properties:
- each point
 of
of  belongs to some set
belongs to some set 
- each two sets
 and
and  are contained in some set
are contained in some set  :
:
-
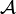 is closed under the operation of multiplication by scalars:
is closed under the operation of multiplication by scalars:
Then the seminorms of the form
define a Hausdorff locally convex topology on 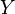 which is called the polar topology[1] on
which is called the polar topology[1] on 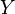 generated by the family of sets
generated by the family of sets 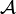 . The sets
. The sets
form a local base of this topology. A net of elements  tends to an element
tends to an element  in this topology if and only if
in this topology if and only if
Because of this the polar topology is often called the topology of uniform convergence on the sets of  . The semi norm
. The semi norm  is the gauge of the polar set
is the gauge of the polar set  .
.
Examples
- if
 is the family of all bounded sets in
is the family of all bounded sets in  then the polar topology on
then the polar topology on 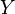 coincides with the strong topology,
coincides with the strong topology, - if
 is the family of all finite sets in
is the family of all finite sets in  then the polar topology on
then the polar topology on 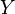 coincides with the weak topology,
coincides with the weak topology, - the topology of an arbitrary locally convex space
 can be described as the polar topology defined on
can be described as the polar topology defined on  by the family
by the family  of all equicontinuous sets
of all equicontinuous sets  in the dual space
in the dual space  .[2]
.[2]
See also
Notes
- ↑ A.P.Robertson, W.Robertson (1964, III.2)
- ↑ In other words,
 iff
iff  and there is a neighbourhood of zero
and there is a neighbourhood of zero  such that
such that 
References
- Robertson, A.P.; Robertson, W. (1964). Topological vector spaces. Cambridge University Press.
- Schaefer, Helmuth H. (1966). Topological vector spaces. New York: The MacMillan Company. ISBN 0-387-98726-6.
| ||||||||||||||||||||||||||||||||||