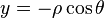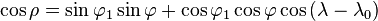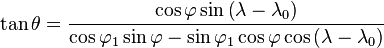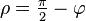Azimuthal equidistant projection


The azimuthal equidistant projection is an azimuthal map projection. It has the useful properties that all points on the map are at proportionately correct distances from the center point, and that all points on the map are at the correct azimuth (direction) from the center point. A useful application for this type of projection is a polar projection which shows all meridians (lines of longitude) as straight, with distances from the pole represented correctly. The flag of the United Nations contains an example of a polar azimuthal equidistant projection.
This projection is used by the USGS in the National Atlas of the United States of America, and for large-scale mapping of Micronesia. It is useful for showing airline distances from center point of projection and for seismic and radio work.
In the case of radio, this projection allows for directional antenna aiming, especially in the case of HF communications. An operator can point the antenna, usually by an electric rotator, simply locating the target in the map and rotating the antenna to the angle indicated by the map. The map should be centered as nearly as possible to the actual antenna location.
Distances and directions to all places are true only from the center point of projection. Distances are correct between points along straight lines through the center. All other distances are incorrect. Distortion of areas and shapes increases with distance from the center point.
Some types of wide-angle camera lenses, known as "fisheye lenses" produce an azimuthal equidistant projection of the photographed scene onto the photographic medium. These lenses allow a much wider field of view than perspective lenses, which are limited to significantly less than 180 degrees.
History
While it may have been used by ancient Egyptians for star maps in some holy books,[1] the earliest text describing the azimuthal equidistant projection is an 11th-century work by al-Biruni.[2]
The projection appears in many Renaissance maps, and Gerardus Mercator used it for an inset of the north polar regions in sheet 13 and legend 6 of his well-known 1569 map. In France and Russia this projection is named "Postel projection" after Guillaume Postel, who used it for a map in 1581.[3] Many modern star chart planispheres use the polar azimuthal equidistant projection.
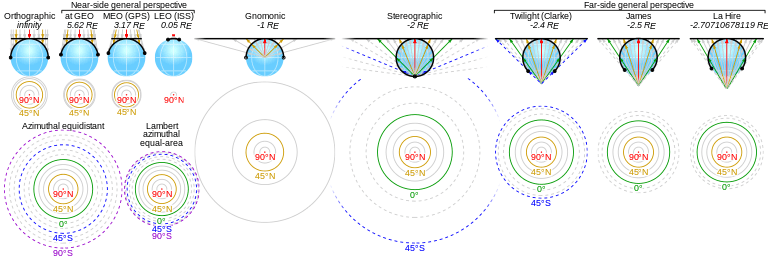
Mathematical definition
A point on the globe is chosen to be special in the sense that mapped distances and azimuths from that point to any other point will be correct. That point, (φ1, λ0), will project to the center of a circular projection, with φ referring to latitude and λ referring to longitude. All points along a given azimuth will project along a straight line from the center, and the angle θ that line subtends from the vertical is the azimuth angle. The distance from the center point to another projected point is given as ρ. By this description, then, the point on the globe specified by (θ,ρ) will be projected to Cartesian coordinates:
The relationship between the coordinates (θ,ρ) of the point on the globe, and its latitude and longitude coordinates (φ, λ) is found as follows. The great circle distance ρ between two points (φ1, λ0) and (φ, λ) on the sphere is given by:[4]
The azimuth from the first to the second point is given by:
When the center point is the north pole, these formulas greatly simplify to:
See also
References
- ↑ SNYDER, John P. (1997). Flattening the earth: two thousand years of map projections. University of Chicago Press. ISBN 0-226-76747-7., p.29
- ↑ David A. KING (1996), "Astronomy and Islamic society: Qibla, gnomics and timekeeping", in Roshdi Rashed, ed., Encyclopedia of the History of Arabic Science, Vol. 1, p. 128–184 [153]. Routledge, London and New York.
- ↑ Snyder 1997, p. 29
- ↑ Snyder, John P. (1989). An Album of Map Projections (PDF). p. 228.
External links
- Table of examples and properties of all common projections, from radicalcartography.net
- Online Azimuthal Equidistant Map Generator
- An interactive Java Applet to study the metric deformations of the Azimuthal Equidistant Projection.
- GeographicLib provides a class for performing azimuthal equidistant projections centered at any point on the ellipsoid.
- Concept and mathematics of the Azimuthal Equidistant Projection for the marine navigator.
- Animated US National Weather Service Wind Data for Azimuthal equidistant projection.