Platt scaling

Machine learning and data mining

Problems
Classification Clustering Regression Anomaly detection Association rules Reinforcement learning Structured prediction Feature engineering Feature learning Online learning Semi-supervised learning Unsupervised learning Learning to rank Grammar induction
Supervised learning (classification • regression)
Decision trees Ensembles (Bagging, Boosting, Random forest) k-NN Linear regression Naive Bayes Neural networks Logistic regression Perceptron Relevance vector machine (RVM) Support vector machine (SVM)
Clustering
BIRCH Hierarchical k-means Expectation-maximization (EM) DBSCAN OPTICS Mean-shift
Dimensionality reduction
Factor analysis CCA ICA LDA NMF PCA t-SNE
Structured prediction
Graphical models (Bayes net, CRF, HMM)
Anomaly detection
k-NN Local outlier factor
Neural nets
Autoencoder Deep learning Multilayer perceptron RNN Restricted Boltzmann machine SOM Convolutional neural network
Theory
Bias-variance dilemma Computational learning theory Empirical risk minimization Occam learning PAC learning Statistical learning VC theory
Machine learning venues
NIPS ICML JMLR ArXiv:cs.LG
Data mining venues
KDD ICDM SDM
Machine learning portal

In machine learning, Platt scaling or Platt calibration is a way of transforming the outputs of a classification model into a probability distribution over classes. The method was invented by John Platt in the context of support vector machines,^[1] replacing an earlier method by Vapnik, but can be applied to other classification models.^[2] Platt scaling works by fitting a logistic regression model to a classifier's scores.

Description

Consider the problem of binary classification: for inputs $x$ , we want to determine whether they belong to one of two classes, arbitrarily labeled $+1$ and $-1$ . We assume that the classification problem will be solved by a real-valued function $f$ , by predicting a class label $y = sign(f (x))$ .^{[lower-alpha 1]} For many problems, it is convenient to get a probability $P(y =1| x)$ , i.e. a classification that not only gives an answer, but also a degree of certainty about the answer. Some classification models do not provide such a probability, or give poor probability estimates.

Platt scaling is an algorithm to solve the aforementioned problem. It produces probability estimates

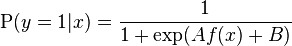\mathrm{P}(y=1 | x) = \frac{1}{1 + \exp(Af(x) + B)}

i.e., a logistic transformation of the classifier scores $f (x)$ , where $A$ and $B$ are two scalar parameters that are learned by the algorithm. Note that predictions can now be made according to $y = 1$ iff $P(y =1| x) > ½$ ; if $B \neq 0$ , the probability estimates contain a correction compared to the old decision function $y = sign(f (x))$ .^[3]

The parameters $A$ and $B$ are estimated using a maximum likelihood method that optimizes on the same training set as that for the original classifier $f$ . To avoid overfitting to this set, a held-out calibration set or cross-validation can be used, but Platt additionally suggests transforming the labels $y$ to target probabilities

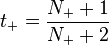t_{+} = \frac{N_{+} + 1}{N_{+} + 2}

for positive samples (

y = 1

), and

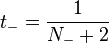t_{-} = \frac{1}{N_{-} + 2}

for negative samples,

y = -1

Here, $N ₊$ and $N ₋$ are the number of positive and negative samples, resp. This transformation follows by applying Bayes' rule to a model of out-of-sample data that has a uniform prior over the labels.^[1]

Platt himself suggested using the Levenberg–Marquardt algorithm to optimize the parameters, but a Newton algorithm was later proposed that should be more numerically stable.^[4]

Analysis

Platt scaling has been shown to be effective for SVMs as well as other types of classification models, including boosted models and even naive Bayes classifiers, which produce distorted probability distributions. It is particularly effective for max-margin methods such as SVMs and boosted trees, which show sigmoidal distortions in their predicted probabilities, but has less of an effect with well-calibrated models such as logistic regression, multilayer perceptrons and random forests.^[2]

An alternative approach to probability calibration is to fit an isotonic regression model to an ill-calibrated probability model. This has been shown to work better than Platt scaling, in particular when enough training data is available.^[2]

Notes

↑ See sign function. The label for $f (x) = 0$ is arbitrarily chosen to be either zero, or one.

References

1 2 Platt, John (1999). "Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods" (PDF). Advances in large margin classifiers 10 (3): 61–74.
1 2 3 Niculescu-Mizil, Alexandru; Caruana, Rich (2005). Predicting good probabilities with supervised learning (PDF). ICML. doi:10.1145/1102351.1102430.
↑ Olivier Chapelle; Vladimir Vapnik; Olivier Bousquet; Sayan Mukherjee (2002). "Choosing multiple parameters for support vector machines" (PDF). Machine Learning 46: 131–159. doi:10.1023/a:1012450327387.
↑ Lin, Hsuan-Tien; Lin, Chih-Jen; Weng, Ruby C. (2007). "A note on Platt’s probabilistic outputs for support vector machines" (PDF). Machine Learning 68 (3): 267–276. doi:10.1007/s10994-007-5018-6.

This article is issued from Wikipedia - version of the Saturday, August 29, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Platt scaling

Description

Analysis

See also

Notes

References