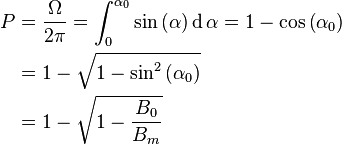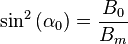Pitch angle (particle motion)

This article is about the pitch angle of a charged particle. For Pitch angle in engineering, see Pitch angle (engineering).

The pitch angle of a charged particle is the angle between the particle's velocity vector and the local magnetic field. This is a common measurement and topic when studying the magnetosphere, magnetic mirrors, ciconic cusps and polywells. See Aurora and Ring current

Usage: particle motion

It is customary to discuss the direction a particle is heading by its pitch angle. A pitch angle of 0 degrees is a particle whose parallel motion is perfectly along the local magnetic field. In the northern hemisphere this particle would be heading down toward the Earth (and the opposite in the southern hemisphere). A pitch angle of 90 degrees is a particle that is locally mirroring (see: Magnetosphere particle motion).

Special case: equatorial pitch angle

The equatorial pitch angle of a particle is the pitch angle of the particle at the Earth's geomagnetic equator. This angle defines the loss cone of a particle. The loss cone is the set of angles where the particle will strike the atmosphere and no longer be trapped in the magnetosphere while particles with pitch angles outside the loss cone will continue to be trapped. The loss cone is defined as the probability of particle loss from the magnetic bottle which is:


\begin{align} P &= \frac{\Omega}{2\pi} = \int_{0}^{\alpha_0} \sin\left(\alpha\right) \operatorname{d}\alpha = 1 - \cos\left(\alpha_0\right) \\ &= 1 - \sqrt{1 - \sin^2\left(\alpha_0\right)} \\ &= 1 - \sqrt{1 - \frac{B_0}{B_m}} \end{align}


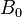Where \Omega is the solid angle we are concerned with, \alpha_0 is the equatorial pitch angle of the particle, B_0 is the equatorial magnetic field strength, and 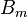B_m is the maximum field strength. Notice that this is independent of charge, mass, or kinetic energy.


The last line in the above derivation is due to the invariance of the invariance of the magnetic moment \mu at the point of reflection:


\mu = \frac{1}{2} \frac{mv^2_{\perp 0}}{B_0} = \frac{1}{2} \frac{mv^2\sin^2\left(\alpha_0\right)}{B_0} = \frac{1}{2} \frac{mv^2}{B_m}

thus


\sin^2\left(\alpha_0\right) = \frac{B_0}{B_m}

See also

External links

This article is issued from Wikipedia - version of the Tuesday, February 25, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.