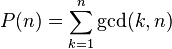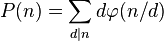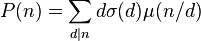Pillai's arithmetical function

In number theory, the gcd-sum function,^[1] also called Pillai's arithmetical function,^[1] is defined for every $n$ by

P(n)=\sum_{k=1}^n\gcd(k,n)

or equivalently^[1]

P(n) = \sum_{d\mid n} d \varphi(n/d)

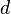where $d$ is a divisor of $n$ and $\varphi$ is Euler's totient function.

it also can be written as^[2]

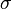P(n) = \sum_{d \mid n} d \sigma(d) \mu(n/d)

where, $\sigma$ is the Divisor function, and 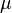$\mu$ is the Möbius function.

This multiplicative arithmetical function was introduced by the Indian mathematician Subbayya Sivasankaranarayana Pillai in 1933.^[3]

References

1 2 3 Lászlo Tóth (2010). "A survey of gcd-sum functions". J. Integer Sequences 13.
↑ http://math.stackexchange.com/questions/135351/sum-of-gcdk-n
↑ S. S. Pillai (1933). "On an arithmetic function". Annamalai University Journal II: 242–248.

A018804

This article is issued from Wikipedia - version of the Monday, January 06, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.