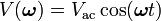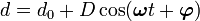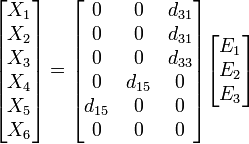Piezoresponse force microscopy

PFM of BaTiO₃ single crystal showing simultaneously acquired topography (top) and domain structure (bottom). The scale bar is 10 μm

Piezoresponse force microscopy (PFM) is a variant of atomic force microscopy (AFM) that allows imaging and manipulation of ferroelectric domains. This is achieved by bringing a sharp conductive probe into contact with a ferroelectric surface (or piezoelectric material) and applying an alternating current (AC) bias to the probe tip in order to excite deformation of the sample through the converse piezoelectric effect (CPE). The resulting deflection of the probe cantilever is detected through standard split photodiode detector methods and then demodulated by use of a lock-in amplifier (LiA). In this way topography and ferroelectric domains can be imaged simultaneously with high resolution.

Basic principles

General overview

Piezoresponse force microscopy is a technique which since its inception and first implementation by Güthner and Dransfeld ^[1] has steadily attracted more and more interest. This is due in large part to the many benefits and few drawbacks that PFM offers researchers in varying fields from ferroelectrics, semiconductors and even biology.^[2] In its most common format PFM allows for identification of domains from relatively large scale e.g. 100×100 µm² scans right down to the nanoscale with the added advantage of simultaneous imaging of sample surface topography. Also possible is the ability to switch regions of ferroelectric domains with the application of a sufficiently high bias to the probe which opens up the opportunity of investigating domain formation on nanometre length scales with nanosecond time resolution.^[3] Many recent advances have expanded the list of applications for PFM and further increased this powerful technique. Indeed what started as a user modified AFM has now attracted the attention of the major SPM manufacturers so much so that in fact many now supply ‘ready-made’ systems specifically for PFM each with novel features for research. This is testament to the growth of the field and reflects the numbers of users throughout the scientific world who are at the forefront of scientific research.

Diagram showing cantilever movements from mechanical deformation of piezoelectric domains

Top line shows an in-phase piezoresponse to the driving voltage and the bottom line shows a 180° out-of-phase piezoresponse to driving voltage. Alignment of electric field and polarisation orientation (top right) results in an expansion of the domain, giving a positive deflection as measured by the photodiode. When the bias is negative the domain contracts giving a negative deflection as measured by the photodiode meaning that the piezoresponse will always be in-phase with the driving voltage. For anti-alignment of electric field and polarisation orientation (bottom right) a positive bias results in a contraction of the domain and so gives a negative deflection as measured by the photodiode therefore the piezoresponse is 180° out-of-phase with the driving voltage. In this way the orientation of polarisation within a domain can be observed.

Consider that a static or DC voltage applied to a piezoelectric surface will produce a displacement but as applied fields are quite low and the piezoelectric tensor coefficients are relatively small then the physical displacement will also be small such that it is below the level of possible detection of the system. Take as an example, the d₃₃ piezoelectric tensor coefficient of BaTiO₃, it has a value of 85.6 pm V⁻¹ meaning that applying 1 V across the material results in a displacement of 85.6 pm or 0.0856 nm, a minute cantilever displacement even for the high precision of AFM deflection detection. In order to separate this low level signal from random noise a lock-in technique is used wherein a modulated voltage reference signal,

V(\boldsymbol\omega)=V_{\mathrm{ac}}\cos(\boldsymbol\omega t) \;

of frequency ω and amplitude V_ac is applied to the tip giving rise to an oscillatory deformation of the sample surface,

d=d_{\mathrm{0}}+D\cos(\boldsymbol\omega t + \boldsymbol\varphi) \;

from the equilibrium position d₀ with amplitude D, and an associated phase difference φ. The resulting movement of the cantilever is detected by the photodiode and so an oscillating surface displacement is converted into an oscillating voltage. A lock-in-amplifier (LiA) is then able to retrieve the amplitude and phase of the CPE induced surface deformation by the process outlined below.

Converse piezoelectric effect

The converse piezoelectric effect (CPE) describes how an applied electric field will create a resultant strain which in turn leads to a physical deformation of the material. This effect can be described through the constitutive equations.^[4] The CPE can be written as

X_{\mathrm{i}}=d_{\mathrm{ki}}E_{\mathrm{k}} \;

where X_i is the strain tensor, d_ki is the piezoelectric tensor, and E_k is the electric field. If the piezoelectric tensor is considered to be that of the tetragonal crystal system (that of BaTiO₃) then it is

\begin{bmatrix} X_1 \\ X_2 \\ X_3 \\ X_4 \\ X_5 \\ X_6 \end{bmatrix} = \begin{bmatrix} 0 & 0 & d_{31} \\ 0 & 0 & d_{31} \\ 0 & 0 & d_{33} \\ 0 & d_{15} & 0 \\ d_{15} & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} E_1 \\ E_2 \\ E_3 \end{bmatrix}

such that the equation will lead to the strain components for an applied field. If the field is applied exclusively in one direction i.e. E₃ for example, then the resulting strain components are: d₃₁E₃, d₃₁E₃, d₃₃E₃

Thus for an electric field applied along the c-axis of BaTiO₃ i.e. E₃, then the resulting deformation of the crystal will be an elongation along the c-axis and an axially symmetric contraction along the other orthogonal directions. PFM uses the effect of this deformation to detect domains and also to determine their orientation.

Conductive probe

The most important property of the probe for use in PFM is that it should be conducting. This is generally required in order to provide a means of applying a bias to the sample, and can be achieved through manufacturing standard silicon probes and coating them in a conductive material. Common coatings are platinum, gold, tungsten and even conductive diamond.

Scanning electron microscope images of increasing magnification of a conductive coated scanning probe

Scanning electron microscopy images of a PtIr₅ coated scanning probe. From left to right shows images of increasing magnification where the scale bar in the first image is 50 μm and in the third is 200 nm. The first image shows the substrate, cantilever and the tip whereas the second image shows the tip geometry whilst the last image shows the tip apex and demonstrates the fine point that is achieved e.g. radius of curvature of less than 40 nm.

Lock-in amplifier

In the general case a lock-in amplifier (LiA) ‘compares’ an input signal against that of a reference signal (either generated internally or supplied by an external function generator) in order to separate the information contained in the input signal at the frequency of the reference signal. This is called demodulation and is done in a number of easy steps. The reference signal 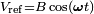$\scriptstyle V_\mathrm{ref}=B\cos(\boldsymbol\omega t)$ , and input signal, 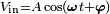$\scriptstyle V_\mathrm{in}=A\cos(\boldsymbol\omega t + \boldsymbol\varphi)$ , are multiplied together to give the demodulator output,

$V_\mathrm{out}=\frac{1}{2}AB\cos(\boldsymbol\varphi)+ \frac{1}{2}AB\cos(2\boldsymbol\omega t +\boldsymbol\varphi)$

where A is the input signal Amplitude and B is the reference signal Amplitude, ω is the frequency of both the reference and input signals, and φ is any phase shift between the two signals.

The above equation has an AC component at twice the frequency of the original signals (second term) and a DC component (first term) whose value is related to both the amplitude and phase of the input signal. The demodulator output is sent through a low-pass filter to remove the 2ω component and leave the DC component then the signal is integrated over a period of time defined as the Time Constant, τ_LiA which is a user-definable parameter. Several different outputs are commonly available from a LiA: X output is the demodulator output and Y is the second demodulator output which is shifted by 90° in reference to the first output, together they hold both the phase, θ, and magnitude, R, information and are given by

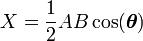$X=\frac{1}{2}AB\cos(\boldsymbol\theta)$ and

$Y=\frac{1}{2}AB\cos(\boldsymbol\theta +\frac{\pi}{2})=\frac{1}{2}AB\sin(\boldsymbol\theta)$

However, phase and amplitude of the input signal can also be calculated and outputted from the LiA if desired, so that the full amount of information is available. The phase output can be determined from the following equation:

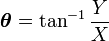
$\boldsymbol\theta=\tan^{-1}\frac{Y}{X}$

The magnitude is then given by:

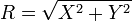
$R=\sqrt{X^2+Y^2}$

This allows R to be calculated even if the input signal differs in phase from the reference signal.

Differentiating vertical and lateral PFM signals

Diagram showing cantilever dynamics and the optical detection through AFM split photodiode detector

Diagrams showing the effect of cantilever movement with the photodetector represented by the square with quadrants labelled A, B, C and D. Torsional bending of the cantilever (left) leads to a change in lateral deflection and (right) vertical displacement of the cantilever leads to a change in vertical deflection

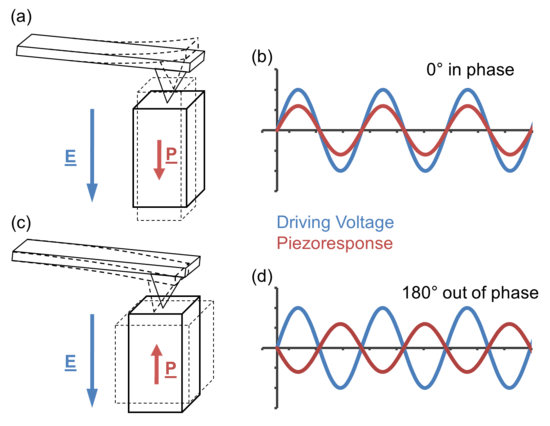
A basic interpretation of PFM (which is generally accepted) identifies that two modes of imaging are possible, one that is sensitive to out-of-plane and one to in-plane piezoresponse, termed, vertical and lateral PFM (VPFM and LPFM) respectively.^[5] The separation of these components is possible through the use of a split photodiode detector, standard to all optical detection AFM systems. In this setup the detector is split into quadrants, nominally A, B, C and D. The centre of the entire detector outputs 0 V but as the laser spot moves a radial distance from this centre point the magnitude of the outputted voltage will increase linearly. A vertical deflection can be defined as {(A+B)-(C+D)}/(ABCD) so that now positive and negative voltages are ascribed to positive and negative cantilever vertical displacements. Similarly a lateral deflection is defined as {(B+D)-(A+C)}/(ABCD) to describe positive and negative torsional movements of the cantilever. So VPFM will utilise the vertical deflection signal from the photodiode detector so will only be sensitive to out-of-plane polar components and LPFM will utilise the lateral deflection signal from the photodiode and will only be sensitive to in-plane polar components.

For polar components orientated such that they are parallel to the electric field the resulting oscillating movement will be entirely in-phase with the modulated electric field but for an anti-parallel alignment the motion will be 180° out-of-phase. In this way it is possible to determine the orientation of the vertical components of polarisation from analysis of the phase information, φ, contained in the input signal, readily available after demodulation in the LiA, when using the VPFM mode. In a similar sense the orientations of in-plane polar components can also be determined from the phase difference when using the LPFM mode. The amplitude of the piezoresponse of either VPFM or LPFM is also given by the LiA, in the form of the magnitude, R.

Examples of PFM imaging

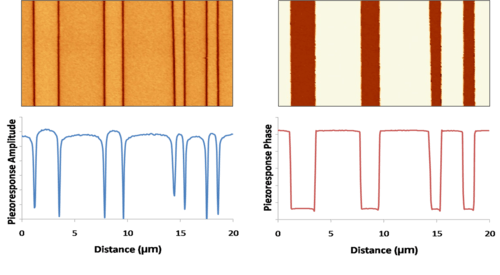
180° ferroelectric domains as imaged by PFM

180° ferroelectric domains in KTP as imaged by PFM. Below are the associated line profiles across the domains

The image shows periodically poled 180° domains in potassium titanyl phosphate (KTP) as imaged by VPFM. In the image piezoresponse amplitude can be seen where dark areas represent the zero amplitude that is expected at domain boundaries where the unit cell is cubic i.e. centrosymmetric and so therefore not ferroelectric. On the left hand side piezoresponse phase can be seen where the measured phase changes to show the out-of-plane components that are pointing out of the screen, white areas, and into the screen, dark areas. The scan area is 20×10 µm². Below each scan is the relevant cross-section that shows in arbitrary units the PR amplitude and phase.

PFM applied to biological materials

PFM has been successfully applied to a range of biological materials such as teeth,^[6] bone, and single collagen fibrils.^[7] It has been hypothesized that the endogenous piezoelectricity in these materials may be relevant in their mechanobiology. For example, using PFM it has been shown that a single collagen fibril as small as 100 nm behaves predominantly as a shear piezoelectric materials with an effective piezoelectric constant of ~1 pm/V.

Advanced PFM modes

Several additions have been made to PFM that substantially increase the flexibility of the technique to probe nanoscale features.

Stroboscopic PFM

Stroboscopic PFM allows for time resolved imaging of switching in pseudo real-time.^[8] A voltage pulse of amplitude much higher than the coercive voltage of the sample but shorter in duration than the characteristic switching time is applied to the sample and subsequently imaged. Further pulses with the same amplitude but longer in time are then applied with regular PFM imaging at the intervals. In this way a series of images showing the switching of the sample can be obtained. Typical pulses are of tens of nanoseconds in duration and are therefore capable of resolving the first nucleation sites of domain reversal and then observing how these sites evolve.

Contact resonance PFM

Remembering that in PFM an AC bias of a certain frequency causes a deformation of the sample material at that same frequency the system can be considered as a driven harmonic oscillator. As such there exists a resonance as a function of driving frequency. This effect has been exploited in PFM to provide an enhancement in the PR signal, thus allowing for a higher signal-to-noise or similar signal-to-noise at lower driving bias amplitude.^[9] Typically this contact resonance is in the kilo- to mega-hertz range which is several times higher in frequency than the first free harmonic in air of the cantilever used. However a drawback is that the contact resonance is dependent not only on the dynamic response of the cantilever but also on the elastic modulus of the sample material immediately in contact with the probe tip and so therefore can change during scanning over different areas. This leads to a change in the measured PR amplitude and so is undesirable. One method of bypassing the inherent disadvantages of contact resonance PFM is to change the driving frequency in order to shadow or track the changes in the frequency of the contact resonance. This feature as developed by Asylum Research called Dual AC™ Resonance Tracking (DART) uses two limit frequencies on either side of the contact resonance peak and so can sense changes in the peak position. It is then possible to adapt the AC bias driving frequency correspondingly in order to maintain the signal boost that results from the contact resonance.

Switching spectroscopy (SS) PFM

In this technique the area underneath the PFM tip is switched with simultaneous acquisition of a hysteresis loop that can be analysed to obtain information about the sample properties.^[10] A series of hysteresis loops are acquired across the sample surface in order to map the switching characteristics as a function of position. In this way an image representing switching properties such as coercive voltage, remnant polarisation, imprint and work of switching amongst others can be displayed in which each pixel displays the desired data from the hysteresis loop acquired at that point. This allows spatial analysis of switching properties to be compared with sample topography.

Advantages and disadvantages

Advantages

High resolution on the nanometer scale
Simultaneous acquisition of topography and piezoresponse
Allows manipulation of ferroelectric domains
Non-destructive
Little sample preparation required

Disadvantages

Scans can be slow, e.g. tens of minutes
Tip wear changes surface interaction and can affect contrast
Limited to lateral range of AFM i.e. approximately 100×100 µm²

References

↑ Güthner, P.; Dransfeld, K. (1992). "Local poling of ferroelectric polymers by scanning force microscopy". Applied Physics Letters 61 (9): 1137–1139. Bibcode:1992ApPhL..61.1137G. doi:10.1063/1.107693.
↑ Rodriguez, B.J.; Kalinin, S.V.; Shin, J.; Jesse, S.; Grichko, V.; Thundat, T.; Baddorf, A.P.; Gruverman, A. (2006). "Electromechanical imaging of biomaterials by scanning probe microscopy" (PDF). Journal of Structural Biology 153 (2): 151–9. doi:10.1016/j.jsb.2005.10.008. PMID 16403652.
↑ Kalinin, Sergei V; Morozovska, Anna N; Chen, Long Qing; Rodriguez, Brian J (2010). "Local polarization dynamics in ferroelectric materials". Reports on Progress in Physics 73 (5): 056502. Bibcode:2010RPPh...73e6502K. doi:10.1088/0034-4885/73/5/056502.
↑ Rosen, C.Z., Hiremath, B.V., Newnham, R. (ed) "Piezoelectricity" American Institute of Physics, Key Papers in Physics, No 5, 227–283 (1992)
↑ Kalinin, SV; Rodriguez, BJ; Jesse, S; Shin, J; Baddorf, AP; Gupta, P; Jain, H; Williams, DB; Gruverman, A (2006). "Vector piezoresponse force microscopy". Microscopy and microanalysis : the official journal of Microscopy Society of America, Microbeam Analysis Society, Microscopical Society of Canada 12 (3): 206–20. Bibcode:2006MiMic..12..206K. doi:10.1017/S1431927606060156. PMID 17481357.
↑ Kalinin, Sergei V.; Rodriguez, B. J.; Jesse, S.; Thundat, T.; Gruverman, A. (2005). "Electromechanical imaging of biological systems with sub-10 nm resolution". Applied Physics Letters 87 (5): 053901. arXiv:cond-mat/0504232. Bibcode:2005ApPhL..87e3901K. doi:10.1063/1.2006984.
↑ Minary-Jolandan, Majid; Yu, Min-Feng (2009). "Uncovering Nanoscale Electromechanical Heterogeneity in the Subfibrillar Structure of Collagen Fibrils Responsible for the Piezoelectricity of Bone" (PDF). ACS Nano 3 (7): 1859–63. doi:10.1021/nn900472n. PMID 19505115.
↑ Gruverman, A.; Rodriguez, B. J.; Dehoff, C.; Waldrep, J. D.; Kingon, A. I.; Nemanich, R. J.; Cross, J. S. (2005). "Direct studies of domain switching dynamics in thin film ferroelectric capacitors". Applied Physics Letters 87 (8): 082902. Bibcode:2005ApPhL..87h2902G. doi:10.1063/1.2010605.
↑ Harnagea, C.; Alexe, M.; Hesse, D.; Pignolet, A. (2003). "Contact resonances in voltage-modulated force microscopy" (PDF). Applied Physics Letters 83 (2): 338. Bibcode:2003ApPhL..83..338H. doi:10.1063/1.1592307.
↑ Rodriguez, Brian J; Jesse, Stephen; Baddorf, Arthur P; Zhao, T; Chu, Y H; Ramesh, R; Eliseev, Eugene A; Morozovska, Anna N; Kalinin, Sergei V (2007). "Spatially resolved mapping of ferroelectric switching behavior in self-assembled multiferroic nanostructures: strain, size, and interface effects". Nanotechnology 18 (40): 405701. Bibcode:2007Nanot..18N5701R. doi:10.1088/0957-4484/18/40/405701.

External links

Asylum Research PFM Application Note

Contact Resonance Application Note

This article is issued from Wikipedia - version of the Friday, November 20, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.