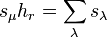Pieri's formula

In mathematics, Pieri's formula, named after Mario Pieri, describes the product of a Schubert cycle by a special Schubert cycle in the Schubert calculus, or the product of a Schur polynomial by a complete symmetric function.

In terms of Schur functions s_λ indexed by partitions λ, it states that

\displaystyle s_\mu h_r=\sum_\lambda s_\lambda

where h_r is a complete homogeneous symmetric polynomial and the sum is over all partitions λ obtained from μ by adding r elements, no two in the same column.

Pieri's formula implies Giambelli's formula. The Littlewood–Richardson rule is a generalization of Pieri's formula giving the product of any two Schur functions. Monk's formula is an analogue of Pieri's formula for flag manifolds.

References

Macdonald, I. G. (1995), Symmetric functions and Hall polynomials, Oxford Mathematical Monographs (2nd ed.), The Clarendon Press Oxford University Press, ISBN 978-0-19-853489-1, MR 1354144
Sottile, Frank (2001), "S/s130080", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

This article is issued from Wikipedia - version of the Thursday, September 25, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.