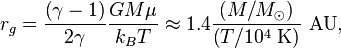Photoevaporation

Photoevaporation denotes the process when a planet is stripped of its atmosphere (or parts of the atmosphere) due to high energy photons and other electromagnetic radiation. If a photon interacts with an atmospheric molecule, the molecule is accelerated and its temperature increased. If sufficient energy is provided, the molecule or atom may reach the escape velocity of the planet and "evaporate" into space. The lower the mass number of the gas, the higher the velocity obtained by interaction with a photon. Thus hydrogen is the gas which is most prone to photoevaporation.
Photoevaporation with protoplanetary disks
Protoplanetary disks can be dispersed by stellar wind and heating due to incident electromagnetic radiation. The radiation interacts with matter and thus accelerates it outwards. This effect is only noticeable when there is sufficient radiation strength, such as coming from nearby O and B type stars or when the central protostar commences nuclear fusion.
The disk is composed of gas and dust. The gas, consisting mostly of light elements such as hydrogen and helium, is mainly affected by the effect, causing the ratio between dust and gas to increase.
Radiation from the central star excites particles in the accretion disk. The irradiation of the disk gives rise to a stability length scale known as the gravitational radius (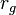 ). Outside of the gravitational radius, particles can become sufficiently excited to escape
the gravity of the disk, and evaporate. After 106 – 107 years,
the viscous accretion rates fall below the photoevaporation rates at
). Outside of the gravitational radius, particles can become sufficiently excited to escape
the gravity of the disk, and evaporate. After 106 – 107 years,
the viscous accretion rates fall below the photoevaporation rates at 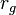 .
A gap then opens around
.
A gap then opens around 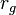 , the inner disk drains onto the central star,
or spreads to
, the inner disk drains onto the central star,
or spreads to 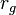 and evaporates. An inner hole extending to
and evaporates. An inner hole extending to 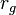 is produced. Once an inner hole forms, the outer disk is very rapidly cleared.
is produced. Once an inner hole forms, the outer disk is very rapidly cleared.
The formula for the gravitational radius of the disk is[1]
where  is the ratio of specific heats (= 5/3 for a monatomic gas),
is the ratio of specific heats (= 5/3 for a monatomic gas),  the universal gravitational constant,
the universal gravitational constant,  the mass of the central star,
the mass of the central star,  the mass of the Sun,
the mass of the Sun,
 the mean weight of the gas,
the mean weight of the gas, 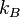 Boltzmann constant,
Boltzmann constant,
 is the temperature of the gas and AU the Astronomical Unit.
is the temperature of the gas and AU the Astronomical Unit.
Because of this effect, the presence of massive stars in a star-forming region is thought to have a great effect on planet formation from the disk around a young stellar object, though it is not yet clear if this effect decelerates or accelerates it.
References
- ↑ Liffman, 2003, "The Gravitational Radius of an Irradiated Disk", Publications of the Astronomical Society of Australia, 20:4:337–339