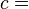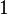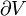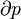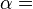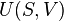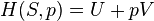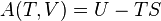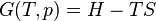Philosophy of thermal and statistical physics

Thermodynamics
The classical Carnot heat engine
Branches Classical Statistical Chemical Equilibrium / Non-equilibrium
Laws Zeroth First Second Third
Systems State Equation of state Ideal gas Real gas State of matter Equilibrium Control volume Instruments Processes Isobaric Isochoric Isothermal Adiabatic Isentropic Isenthalpic Quasistatic Polytropic Free expansion Reversibility Irreversibility Endoreversibility Cycles Heat engines Heat pumps Thermal efficiency
System properties Note: Conjugate variables in italics Property diagrams Intensive and extensive properties Functions of state Temperature / Entropy (introduction) Pressure / Volume Chemical potential / Particle number Vapor quality Reduced properties Process functions Work Heat
Material properties Property databases Specific heat capacity  Compressibility  Thermal expansion
Equations Carnot's theorem Clausius theorem Fundamental relation Ideal gas law Maxwell relations Onsager reciprocal relations Bridgman's equations Table of thermodynamic equations
Potentials Free energy Free entropy Internal energy Enthalpy Helmholtz free energy Gibbs free energy
History Culture History General Heat Entropy Gas laws "Perpetual motion" machines Philosophy Entropy and time Entropy and life Brownian ratchet Maxwell's demon Heat death paradox Loschmidt's paradox Synergetics Theories Caloric theory Theory of heat Vis viva ("living force") Mechanical equivalent of heat Motive power Key publications "An Experimental Enquiry Concerning ... Heat" "On the Equilibrium of Heterogeneous Substances" "Reflections on the Motive Power of Fire" Timelines Thermodynamics Heat engines Art Education Maxwell's thermodynamic surface Entropy as energy dispersal
Scientists Bernoulli Carnot Clapeyron Clausius Carathéodory Duhem Gibbs von Helmholtz Joule Maxwell von Mayer Onsager Rankine Smeaton Stahl Thompson Thomson Waterston
Book:Thermodynamics

The philosophy of thermal and statistical physics is that part of the philosophy of physics whose subject matter is classical thermodynamics, statistical mechanics, and related theories. Its central questions include: What is entropy, and what does the second law of thermodynamics say about it? Does either thermodynamics or statistical mechanics contain an element of time-irreversibility? If so, what does statistical mechanics tell us about the arrow of time?

What is thermodynamics?

Thermodynamics is the study of the macroscopic behaviour of physical systems under the influence of exchange of work and heat with other systems or their environment. It is not concerned with the microscopic properties of these systems, such as the movements of atoms.

At the very heart of contemporary thermodynamics lies the idea of thermodynamic equilibrium, a state in which no macroscopic properties of the system change over time. In orthodox versions of thermodynamics, properties such as temperature and entropy are defined for equilibrium states only. The idea of the existence of states of thermodynamic equilibrium has been central but tacit to thermodynamics. It has recently been dubbed the "minus first law of thermodynamics".^[1][2]

The laws of thermodynamics

Traditionally, thermodynamics has often been described as a "theory of principle". This is a theory in which a few empirical generalisations are taken for granted, and from them the rest of the theory is deduced. According to this view, there is a strong correspondence between three empirical facts and the first three laws of thermodynamics. There is a fourth law, not discussed here.

The zeroth law

Two systems are said to be in thermal equilibrium when 1) both of the systems are in equilibrium, and 2) they remain in equilibrium when they are brought into contact, where 'contact' is meant to imply the possibility of exchanging heat, but not work or particles. Thermal equilibrium is:

• Reflexive: Any system is in thermal equilibrium with itself;
• Symmetric: if system A is in thermal equilibrium with system B, then it is also the case that B is in equilibrium with A;
• Transitive: It is an empirical fact that if system A is in thermal equilibrium with system B, and system B is in thermal equilibrium with system C, then system A and system C are also in thermal equilibrium.

Hence thermal equilibrium between systems is an equivalence relation, and this is the substance of the zeroth law of thermodynamics. According to Max Planck, who wrote an influential textbook on thermodynamics, and many other authors, this empirical principle shows that we can define the "temperature function" central to our everyday conception of heat.

The first law

In simplest terms, the First Law states that the internal energy level of an isolated system is a constant. In the context of a non-isolated system, this law requires that when there is a change in energy when going from one equilibrium state to another, that change is equal to the heat transfer into the system minus the work done by the system. Hence energy in minus energy out equals the change in energy.

The understanding of the First Law embodied in classical physics can be summarized by the saying: "Energy can be neither created nor destroyed."

Because of the:

• Mass-energy equivalence that is a consequence of special relativity (famously summarised for particles at rest by the equation E=mc².);
• Standard Model of particle physics;
• Spontaneous emergence of elementary particles out of the vacuum, as explained by quantum theory, and the equally spontaneous decay of single particles and the mutual annihilation of particles and anti-particles,

the above classical version of the First Law must be amended as follows:

"The total energy of the universe, including the energy equivalent of all baryons, bosons, and leptons in the universe, is constant for all time."

The second law of thermodynamics

In a general sense, the Second Law says that temperature differences between systems in contact with each other tend to even out and that work can be obtained from these non-equilibrium differences, but that loss of heat occurs in the form of entropy when work is done. This law follows simply from statistics: if a physical system is given (is allowed to occupy) new energy states which are equivalent to the existing states (say, a gas is expanding into a larger volume), then the system will occupy "new" states on equal footing with the existing ("old") ones. This is the central postulate of statistical mechanics - that equivalent energy states cannot be distinguished (at equilibrium). Thus, as the number of energy states increases, the energy of the system will be spread among more and more states, thereby increasing the entropy of the system.

The Second Law can be summarized by either of the following sayings:

• "The entropy of any closed thermodynamic system cannot decrease."
• "The entropy of the universe cannot decrease."

Some wags have proposed the following summary of the First and Second Laws: "The first law says you can't win, the second law says you can't even break even."

There are various interpretations of the Second Law, one being Boltzmann's H-theorem.

Maxwell's Demon

James Clerk Maxwell, in an 1871 essay titled the "Theory of Heat," proposed a thought experiment showing why the Second Law might just be a temporary condition, why entropy might be beatable. This thought experiment came to be called Maxwell's Demon.

"If we conceive a being whose faculties are so sharpened that he can follow every molecule in its course, such a being, whose attributes are still essentially finite as our own, would be able to do what is at present impossible for us," (J. C. Maxwell, )

He went on to explain that the demon working at a microscopic level, could operate a gate (presumably of low-friction construction) allowing only swift molecules to pass through it. In this way, the demon's work would result in slow molecules (i.e. cold) on one side of the gated barrier, and heat on the other side. Yet movement from uniformity of temperature to a split of hot/cold violates the Second Law.

In the 20th century, advances in information theory and thermodynamics eventually showed how the proverbial demon's measuring and manipulating activities would necessarily increase total entropy by more than his actions decreased the entropy of the closed gaseous system. Hence Maxwell's demon could not decrease total entropy even in principle, and Maxwell's proposed exception to the Second Law stands refuted.

See also

• Maximum entropy thermodynamics
• Social Thermodynamics Theory

References

• Uffink, J., 2001, "Bluff your way in the second law of thermodynamics," Studies in History and Philosophy of Modern Physics' 32(3): 305-94.
• --------, 2007, "Compendium of the Foundations of Classical Statistical Physics" in Butterfield, J., and John Earman, eds., Philosophy of Physics, Part B. North Holland: 923-1074.
• Valev, P., 2002, "The Law of Self-Acting Machines and Irreversible Processes with reversible Replicas," in Sheehan, D., (ed.) Proceedings of the First International conference on Quantum Limits to the Second Law, American Institute of Physics: 430-35.

External links

• Stanford Encyclopedia of Philosophy: Uffink, Jos (2004). "Boltzmann's Work in Statistical Physics". Retrieved 2007-06-11.