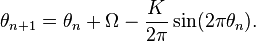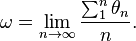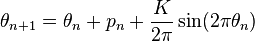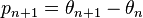Arnold tongue

"Mode lock" redirects here. For other uses, see Mode-locking.
"Mode lock" redirects here. For other uses, see Inharmonicity § Mode-locking.
Circle map showing mode-locked regions or Arnold tongues in black. Ω varies from 0 to 1 along the x-axis, and K varies from 0 at the bottom to 4π at the top.
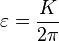
Some of the Arnold tongues for the standard circle map, \varepsilon=\frac{K}{2\pi}
Rotation number as a function of Ω with K held constant at K = 1
Rotation number, with black corresponding to 0, green to 1/2 and red to 1. Ω varies from 0 to 1 along the x-axis, and K varies from 0 at the bottom to 2π at the top.
Bifurcation diagram for Ω held fixed at 1/3, and K running from 0 at bottom to 4π at top. Black regions correspond to Arnold tongues.

In mathematics, particularly in dynamical systems theory, an Arnold tongue of a finite-parameter family of circle maps, named after Vladimir Arnold, is a region in the space of parameters where the map has locally-constant rational rotation number. In other words, it is a level set of a rotation number with nonempty interior.

Standard circle map

Arnold tongues were first investigated for a family of dynamical systems on the circle first defined by Andrey Kolmogorov. Kolmogorov proposed this family as a simplified model for driven mechanical rotors (specifically, a free-spinning wheel weakly coupled by a spring to a motor). These circle map equations also describe a simplified model of the phase-locked loop in electronics. The map exhibits certain regions of its parameters where it is locked to the driving frequency (phase-locking or mode-locking in the language of electronic circuits). Among other applications, the circle map has been used to study the dynamical behaviour of a beating heart.

The circle map is given by iterating the map

\theta_{n+1}=\theta_n + \Omega -\frac{K}{2\pi} \sin (2\pi \theta_n).

where \theta is to be interpreted as polar angle such that its value lies between 0 and 1.

It has two parameters, the coupling strength K and the driving phase Ω. As a model for phase-locked loops, Ω may be interpreted as a driving frequency. For K = 0 and Ω irrational, the map reduces to an irrational rotation.

Mode locking

For small to intermediate values of K (that is, in the range of K = 0 to about K = 1), and certain values of Ω, the map exhibits a phenomenon called mode locking or phase locking. In a phase-locked region, the values 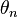\theta_n advance essentially as a rational multiple of n, although they may do so chaotically on the small scale.

The limiting behavior in the mode-locked regions is given by the rotation number

\omega=\lim_{n\to\infty}\frac{\sum_{1}^{n}\theta_n}{n}.

which is also sometimes referred to as the map winding number.

The phase-locked regions, or Arnold tongues, are illustrated in yellow in the figure above. Each such V-shaped region touches down to a rational value 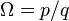\Omega=p/q in the limit of 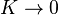K\to 0. The values of (K,Ω) in one of these regions will all result in a motion such that the rotation number 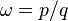\omega=p/q. For example, all values of (K,Ω) in the large V-shaped region in the bottom-center of the figure correspond to a rotation number of 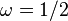\omega=1/2. One reason the term "locking" is used is that the individual values 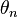\theta_n can be perturbed by rather large random disturbances (up to the width of the tongue, for a given value of K), without disturbing the limiting rotation number. That is, the sequence stays "locked on" to the signal, despite the addition of significant noise to the series 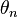\theta_n. This ability to "lock on" in the presence of noise is central to the utility of the phase-locked loop electronic circuit.

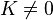There is a mode-locked region for every rational number p/q. It is sometimes said that the circle map maps the rationals, a set of measure zero at K = 0, to a set of non-zero measure for K\neq 0. The largest tongues, ordered by size, occur at the Farey fractions. Fixing K and taking a cross-section through this image, so that ω is plotted as a function of Ω, gives the "Devil's staircase", a shape that is generically similar to the Cantor function.

The circle map also exhibits subharmonic routes to chaos, that is, period doubling of the form 3,6,12,24,....

Chirikov standard map

The Chirikov standard map is related to the circle map, having similar recurrence relations, which may be written as

\theta_{n+1} = \theta_{n} + p_{n} + {\frac K {2\pi}} \sin(2\pi\theta_{n})
p_{n+1} = \theta_{n+1} - \theta_{n}

with both iterates taken modulo 1. In essence, the standard map introduces a momentum 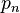p_{n} which is allowed to dynamically vary, rather than being forced fixed, as it is in the circle map. The standard map is studied in physics by means of the kicked rotor Hamiltonian.

References

External links

This article is issued from Wikipedia - version of the Sunday, September 13, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.