Perturbative QCD
Perturbative QCD is a subfield of particle physics in which the theory of strong interactions, Quantum Chromodynamics (QCD), is studied by using the fact that the strong coupling constant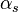 
is small in high energy or short distance interactions, thus allowing Perturbation theory techniques to be applied. In most circumstances, making testable predictions with QCD is extremely difficult, due to the infinite number of topologically inequivalent interactions possible. Over short distances, the coupling is small enough that this infinite number of terms can be approximated accurately by a much more manageable number of terms. Although limited in scope, this approach has resulted in the most precise tests of QCD to date.
The first and most clear test of Perturbative QCD is R measurement in e+e− annihilation. R is defined as the ratio of production rate for e+ + e− → Hadrons to that for e+ + e− → μ+ + μ−. Since only the total production rate is considered, summation over all final state hadrons canceled the dependence on specific hadron type, and this R ratio can be calculated in Perturbative QCD strictly.
Unfortunately, most of the processes can not be calculated directly with Perturbative QCD, since one cannot observe free quarks and gluons due to color confinement - the hadron structure has a nonperturbative nature. Fortunately, physicists developed the QCD factorization theorem, which separates the cross section into two parts: the process dependent Perturbative QCD calculable short-distance parton cross section, and the universal long-distance functions. Those universal long-distance functions can be measured with global fit to experiments. In such a way, scientists obtained a partly calculable prediction to particle reaction processes.
The universal long-distance functions include the parton distribution functions, fragmentation functions, multi-parton correlation functions, generalized parton distribution, generalized distribution amplitude and many kinds of form factors. There are several collaborations for each kind of universal long-distance functions. They have become an important part of modern particle physics.