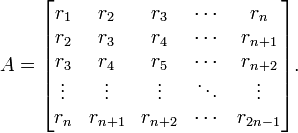Persymmetric matrix

In mathematics, persymmetric matrix may refer to:

  1. a square matrix which is symmetric in the northeast-to-southwest diagonal; or
  2. a square matrix such that the values on each line perpendicular to the main diagonal are the same for a given line.

The first definition is the most common in the recent literature. The designation "Hankel matrix" is often used for matrices satisfying the property in the second definition.

Definition 1

Symmetry pattern of a persymmetric 5×5 matrix

Let A = (aij) be an n × n matrix. The first definition of persymmetric requires that

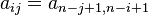a_{ij} = a_{n-j+1,n-i+1} for all i, j.[1]

For example, 5-by-5 persymmetric matrices are of the form

A = \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} & a_{15} \\ a_{21} & a_{22} & a_{23} & a_{24} & a_{14} \\ a_{31} & a_{32} & a_{33} & a_{23} & a_{13} \\ a_{41} & a_{42} & a_{32} & a_{22} & a_{12} \\ a_{51} & a_{41} & a_{31} & a_{21} & a_{11} \end{bmatrix}.

This can be equivalently expressed as AJ = JAT where J is the exchange matrix.

A symmetric matrix is a matrix whose values are symmetric in the northwest-to-southeast diagonal. If a symmetric matrix is rotated by 90°, it becomes a persymmetric matrix. Symmetric persymmetric matrices are sometimes called bisymmetric matrices.

Definition 2

For more details on this topic, see Hankel matrix.

The second definition is due to Thomas Muir.[2] It says that the square matrix A = (aij) is persymmetric if aij depends only on i + j. Persymmetric matrices in this sense, or Hankel matrices as they are often called, are of the form

A = \begin{bmatrix} r_1 & r_2 & r_3 & \cdots & r_n \\ r_2 & r_3 & r_4 & \cdots & r_{n+1} \\ r_3 & r_4 & r_5 & \cdots & r_{n+2} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ r_n & r_{n+1} & r_{n+2} & \cdots & r_{2n-1} \end{bmatrix}.

A persymmetric determinant is the determinant of a persymmetric matrix.[2]

A matrix for which the values on each line parallel to the main diagonal are constant, is called a Toeplitz matrix.

See also

References

  1. ↑ Golub, Gene H.; Van Loan, Charles F. (1996), Matrix Computations (3rd ed.), Baltimore: Johns Hopkins, ISBN 978-0-8018-5414-9. See page 193.
  2. 1 2 Muir, Thomas (1960), Treatise on the Theory of Determinants, Dover Press, p. 419
This article is issued from Wikipedia - version of the Sunday, November 08, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.