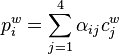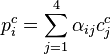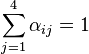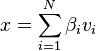Perspective-n-Point
Perspective-n-Point is the problem of estimating the pose of a calibrated camera given a set of n 3D points in the world and their corresponding 2D projections in the image. The camera pose consists of 6 degrees-of-freedom (DOF) which are made up of the rotation (roll, pitch, and yaw) and 3D translation of the camera with respect to the world. This problem originates from camera calibration and has many applications in computer vision and other areas, including 3D pose estimation, robotics and augmented reality. A commonly used solution to the problem exists for n = 3 called P3P, and many solutions are available for the general case of n ≥ 3. Implementations of these solutions are also available in open source software.
Problem Specification
Definition
Given a set of n 3D points in a world reference frame and their corresponding 2D image projections as well as the calibrated intrinsic camera parameters, determine the 6 DOF pose of the camera in the form of its rotation and translation with respect to the world. This follows the perspective project model for cameras:
![s\,p_c = K\,[\,R\, |\, T\, ]\, p_w](../I/m/f197902a02767d877bd9a95aa9655764.png) .
.
where 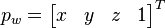 is the homogeneous world point,
is the homogeneous world point, 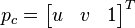 is the corresponding homogeneous image point,
is the corresponding homogeneous image point, 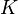 is the matrix of intrinsic camera parameters, (where
is the matrix of intrinsic camera parameters, (where 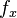 and
and  are the scaled focal lengths,
are the scaled focal lengths, 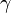 is the skew parameter which is sometimes assumed to be 0, and
is the skew parameter which is sometimes assumed to be 0, and 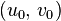 is the principal point),
is the principal point),  is a scale factor for the image point, and
is a scale factor for the image point, and  and
and  are the desired 3D rotation and 3D translation of the camera (extrinsic parameters) that are being calculated. This leads to the following equation for the model:
are the desired 3D rotation and 3D translation of the camera (extrinsic parameters) that are being calculated. This leads to the following equation for the model:
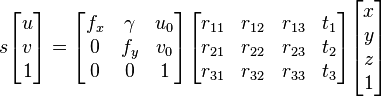 .
.
Assumptions and Data Characteristics
There are a few preliminary aspects of the problem that are common to all solutions of PnP. The assumption made in most solutions is that the camera is already calibrated. Thus, its intrinsic properties are already known, such as the focal length, principal image point, skew parameter, and other parameters. Some methods, such as UPnP.[1] or the Direct Linear Transform (DLT) applied to the projection model, are exceptions to this assumption as they estimate these intrinsic parameters as well as the extrinsic parameters which make up the pose of the camera that the original PnP problem is trying to find.
For each solution to PnP, the chosen point correspondences cannot be coplanar. In addition, PnP can have multiple solutions, and choosing a particular solution would require post-processing of the solution set. Furthermore, using more point correspondences can reduce the impact of noisy data when solving PnP. RANSAC is also commonly used with a PnP method to make the solution robust to outliers in the set of point correspondences. Most methods, however, assume that the data is noise-free.
Methods
This following section describes two common methods that can be used to solve the PnP problem that are also readily available in open source software and how RANSAC can be used to deal with outliers in the data set.
P3P
When n = 3, the PnP problem is in its minimal form of P3P and can be solved with three point correspondences. However, with just three point correspondences, P3P yields many solutions, so a fourth correspondence is used in practice to remove ambiguity. The setup for the problem is as follows.
Let P be the center of projection for the camera, A, B, and C be 3D world points with corresponding images points u, v, and w. Let X = |PA|, Y = |PB|, Z = |PC|, 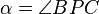 ,
, 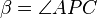 ,
, 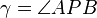 ,
, 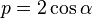 ,
, 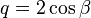 ,
, 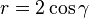 ,
, 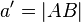 ,
, 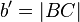 ,
, 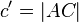 . This forms triangles PBC, PAC, and PAB from which we obtain the equation system for P3P:
. This forms triangles PBC, PAC, and PAB from which we obtain the equation system for P3P:
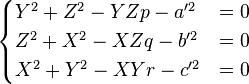 .
.
It's common to normalize the image points before solving P3P. Solving the P3P system results in four possible solutions for R and T. The fourth world point D and its corresponding image point zare then used to to find the best solution among the four. The algorithm for solving the problem as well as the complete solution classification for it is given in the 2003 IEEE Transactions on Pattern Analysis and Machine Intelligence paper by Gao, et. al.[2] An open source implementation of the P3P can be found in OpenCV's calib3d module in the solvePnP function.[3]
EPnP
Efficient PnP (EPnP) is a method developed by Lepetit, et. al in their 2008 International Journal of Computer Vision paper[4] that solves the general problem of PnP for n ≥ 3. This method is based on the notion that each of the n points (which are called reference points) can be expressed as a weighted sum of four virtual control points. Thus, the coordinates of these control points become the unknowns of the problem. It is from these control points that the final pose of the camera is solved for.
As an overview of the process, first note that each of the n reference points in the world frame, 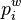 , and their corresponding image points,
, and their corresponding image points, 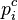 , are weighted sums of the four controls points,
, are weighted sums of the four controls points, 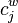 and
and 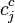 respectively, and the weights are normalized per reference point as shown below. All points are expressed in homogeneous form.
respectively, and the weights are normalized per reference point as shown below. All points are expressed in homogeneous form.
From this, the derivation of the image reference points becomes
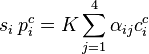 .
.
The homogeneous image control point has the form 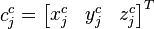 . Rearranging the image reference point equation yields the following two linear equations for each reference point:
. Rearranging the image reference point equation yields the following two linear equations for each reference point:
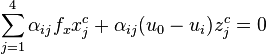
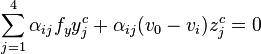 .
.
Using these two equations for each of the n reference points, the system 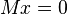 can be formed where
can be formed where 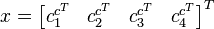 . The solution for the control points exists in the null space of M and is expressed as
. The solution for the control points exists in the null space of M and is expressed as
where  is the number of null singular values in
is the number of null singular values in  and each
and each  is the corresponding right singular vector of
is the corresponding right singular vector of  .
.  can range from 1 to 4. After calculating the initial coefficients
can range from 1 to 4. After calculating the initial coefficients  , the Gauss-Newton algorithm is used to refine them. The R and T matrices that minimize the reprojection error of the world reference points,
, the Gauss-Newton algorithm is used to refine them. The R and T matrices that minimize the reprojection error of the world reference points, 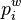 , and their corresponding actual image points
, and their corresponding actual image points 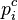 , are then calculated.
, are then calculated.
This solution has  complexity and works in the general case of PnP for both planar and non-planar control points. Open source software implementations of this method can be found in OpenCV's Camera Calibration and 3D Reconstruction module in the solvePnP function[5] as well as from the code published by Lepetit, et. al at their website, CVLAB at EPFL.[6]
complexity and works in the general case of PnP for both planar and non-planar control points. Open source software implementations of this method can be found in OpenCV's Camera Calibration and 3D Reconstruction module in the solvePnP function[5] as well as from the code published by Lepetit, et. al at their website, CVLAB at EPFL.[6]
Using RANSAC
PnP is prone to errors if there are outliers in the set of point correspondences. Thus, RANSAC can be used in conjunction with existing solutions to make the final solution for the camera pose more robust to outliers. An open source implementation of PnP methods with RANSAC can be found in OpenCV's Camera Calibration and 3D Reconstruction module in the solvePnPRansac function[7]
See also
References
- ↑ Penate-Sanchez, A.; Andrade-Cetto, J.; Moreno-Noguer, F. (2013). "Exhaustive Linearization for Robust Camera Pose and Focal Length Estimation". IEEE Transactions on Pattern Analysis and Machine Intelligence 35 (10): 2387–2400. doi:10.1109/TPAMI.2013.36.
- ↑ Gao, Xiao-Shan; Hou, Xiao-Rong; Tang, Jianliang; Cheng, Hang-Fei (2003). "Complete Solution Classification for the Perspective-Three-Point Problem". IEEE Transactions on Pattern Analysis and Machine Intelligence 25 (8): 930–943.
- ↑ "Camera Calibration and 3D Reconstruction". OpenCV.
- ↑ Lepetit, V.; Moreno-Noguer, M.; Fua, P. (2009). "EPnP: An Accurate O(n) Solution to the PnP Problem". International Journal of Computer Vision 81 (2): 155–166.
- ↑ "Camera Calibration and 3D Reconstruction". OpenCV.
- ↑ "EPnP: Efficient Perspective-n-Point Camera Pose Estimation". EPFL-CVLAB.
- ↑ "Camera Calibration and 3D Reconstruction". OpenCV.