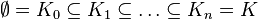Persistent homology

See homology for an introduction to the notation.

Persistent homology is a method for computing topological features of a space at different spatial resolutions. More persistent features are detected over a wide range of length and are deemed more likely to represent true features of the underlying space, rather than artifacts of sampling, noise, or particular choice of parameters.[1]

To find the persistent homology of a space, the space must first be represented as a simplicial complex. A distance function on the underlying space corresponds to a filtration of the simplicial complex, that is a nested sequence of increasing subsets.

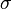Formally, consider a real-valued function on a simplicial complex f:K \rightarrow \mathbb{R} that is non-decreasing on increasing sequences of faces, so f(\sigma) \leq f(\tau) whenever \sigma is a face of 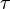\tau in K. Then for every a \in \mathbb{R} the sublevel set K(a)=f^{-1}(-\infty, a] is a subcomplex of K, and the ordering of the values of f on the simplices in K (which is in practice always finite) induces an ordering on the sublevel complexes that defines the filtration

\emptyset = K_0 \subseteq K_1 \subseteq \ldots \subseteq K_n = K

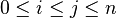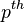When 0\leq i \leq j \leq n, the inclusion K_i \hookrightarrow K_j induces a homomorphism f_p^{i,j}:H_p(K_i)\rightarrow H_p(K_j) on the simplicial homology groups for each dimension p. The p^{th} persistent homology groups are the images of these homomorphisms, and the 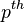p^{th} persistent Betti numbers 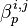\beta_p^{i,j} are the ranks of those groups.[2] Persistent Betti numbers for p=0 coincide with the predecessor of persistence homology, i.e. the size function.[3]

There are various software packages for computing persistence intervals of a finite filtration, such as javaPlex, Dionysus, Perseus, PHAT, DIPHA, Gudhi, and the phom and TDA R packages.

See also

References

  1. ↑ Carlsson, Gunnar (2009). "Topology and data". AMS Bulletin 46(2), 255–308.
  2. ↑ Edelsbrunner, H and Harer, J (2010). Computational Topology: An Introduction. American Mathematical Society.
  3. ↑ Verri, A, Uras, C, Frosini, P and Ferri, M (1993). On the use of size functions for shape analysis, Biological Cybernetics, 70, 99–107.
This article is issued from Wikipedia - version of the Sunday, January 03, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.