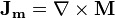Persistent current

Persistent current is a perpetual electric current, not requiring an external power source.

In magnetized objects

In electromagnetism, all magnetizations can be seen as microscopic persistent currents. By definition a magnetization 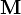\mathbf{M} can be replaced by its corresponding microscopic form, which is an electric current density:

\mathbf{J_m} = \nabla\times\mathbf{M}

This current is a bound current, not having any charge accumulation associated with it since it is divergenceless. What this means is that any permanently magnetized object, for example a piece of lodestone, can be considered to have persistent electric currents running throughout it (the persistent currents are generally concentrated near the surface).

The converse is also true: any persistent electric current is divergence-free, and can therefore be represented instead by a magnetization. Therefore in the macroscopic Maxwell's equations, it is purely a choice of mathematical convenience, whether to represent persistent currents as magnetization or vice versa. In the microscopic formulation of Maxwell's equations, however, 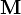\mathbf{M} does not appear and so any magnetizations must be instead represented by bound currents.

Persistent currents in superconductors

In superconductors, charge can flow without any resistance. It is possible to make pieces of superconductor with a large built-in persistent current, either by creating the superconducting state (cooling the material) while charge is flowing through it, or by changing the magnetic field around the superconductor after creating the superconducting state.[1] This principle is used in superconducting electromagnets to generate sustained high magnetic fields that only require a small amount of power to maintain. The persistent current was first identified by Onnes, and attempts to set a lower bound on their duration have reached values of over 100,000 years.[2]

Persistent currents in resistive conductors

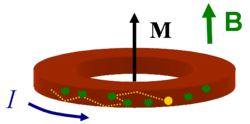
Persistent current schematic. The green arrow indicates the direction of static applied magnetic field B which allows a net current I (blue arrow) to flow and create a magnetization M (black arrow) by breaking the symmetry between clockwise and counterclockwise currents. The yellow dot represents an electron traversing the disordered material of the ring (green stars) without dissipation. A typical ring current is 1 nanoampere for a ring diameter of 0.6 micrometer at a temperature below 0.5 kelvin.[3]

Surprisingly, it is also possible to have tiny persistent currents inside resistive metals that are placed in a magnetic field, even in metals that are nominally "non-magnetic".[4] The current is the result of a quantum mechanical effect that influences how electrons travel through metals, and arises from the same kind of motion that allows the electrons inside an atom to orbit the nucleus forever.

This type of persistent current is a mesoscopic low temperature effect: the magnitude of the current becomes appreciable when the size of the metallic system is reduced to the scale of the electron quantum phase coherence length and the thermal length. Persistent currents decrease with increasing temperature and will vanish exponentially above a temperature known as the Thouless temperature. This temperature scales as the inverse of the circuit diameter squared.[3] Consequently, it has been suggested that persistent currents could flow up to room temperature and above in nanometric metal structures such as metal (Au, Ag,...) nanoparticles. This hypothesis has been offered for explaining the singular magnetic properties of nanoparticles made of gold and other metals.[5] Unlike with superconductors, these persistent currents do not appear at zero magnetic field, as the current fluctuates symmetrically between positive and negative values; the magnetic field breaks that symmetry and allows a nonzero average current. Although the persistent current in an individual ring is largely unpredictable due to uncontrolled factors like the disorder configuration, it has a slight bias so that an average persistent current appears even for an ensemble of conductors with different disorder configurations.[6]

This kind of persistent current was first predicted to be experimentally observable in micrometer-scale rings in 1983 by Markus Büttiker, Yoseph Imry, and Rolf Landauer.[7] Because the effect requires the phase coherence of electrons around the entire ring, the current can not be observed when the ring is interrupted by an ammeter and thus the current must by measured indirectly through its magnetization. In fact, all metals exhibit some magnetization in magnetic fields due a combination of de Haas–van Alphen effect, core diamagnetism, Landau diamagnetism, Pauli paramagnetism, which all appear regardless of the shape of the metal. The additional magnetization from persistent current becomes strong with a connected ring shape, and for example would disappear if the ring were cut.[6]

Experimental evidence of the observation of persistent currents were first reported in 1990 by a research group at Bell Laboratories using a superconducting resonator to study an array of copper rings.[8] Subsequent measurements using superconducting resonators and extremely sensitive magnetometers known as superconducting quantum interference devices (SQUIDs) produced inconsistent results.[9] In 2009, physicists at Stanford University using a scanning SQUID[10] and at Yale University using microelectromechanical cantilevers[3] reported measurements of persistent currents in nanoscale gold and aluminum rings respectively that both showed a strong agreement with the simple theory for non-interacting electrons.

"These are ordinary, non-superconducting metal rings, which we typically think of as resistors, yet these currents will flow forever, even in the absence of an applied voltage."

— Jack Harris, Associate Professor of Physics and Applied Physics at Yale.

The 2009 measurements both reported greater sensitivity to persistent currents than previous measurements and made several other improvements to persistent current detection. The scanning SQUID's ability to change the position of the SQUID detector relative to the ring sample allowed for a number of rings to be measured on one sample chip and better extraction of the current signal from background noise. The cantilever detector's mechanical detection technique made it possible to measure the rings in a clean electromagnetic environment over a large range of magnetic field and also to measure a number of rings on one sample chip.[11]

See also

References

  1. ↑ Yen, F.; Chen, X.; Wang, R. B.; Zhu, J. M.; Li, J.; Ma, G. T. (2013). "Induced Currents in Closed-Ended Type-II Superconducting Coils". IEEE Trans. Appl. Supercond. 23 (6): 8202005. doi:10.1109/TASC.2013.2273534.
  2. ↑ File J, Mills, R Physical Review Letters 1963
  3. 1 2 3 Bleszynski-Jayich, A. C.; Shanks, W. E.; Peaudecerf, B.; Ginossar, E.; von Oppen, F.; Glazman, L.; Harris, J. G. E. (2009). "Persistent Currents in Normal Metal Rings". Science 326 (5950): 272–5. Bibcode:2009Sci...326..272B. doi:10.1126/science.1178139. PMID 19815772.
  4. ↑ "Measuring elusive "persistent current" that flows forever". R&D Daily. October 12, 2009.
  5. ↑ Gréget, Romain (2012). "Magnetic Properties of Gold Nanoparticles: A Room-Temperature Quantum Effect". ChemPhysChem. doi:10.1002/cphc.201200394.
  6. 1 2 Akkermans, Eric; Montambaux, Gilles (2007). Mesoscopic Physics of Electrons and Photons. Cambridge University Press. ISBN 978-0-521-85512-9.
  7. ↑ Büttiker, M.; Imry, Y.; Landauer, R. (1983). "Josephson behavior in small normal one-dimensional rings". Phys. Lett. A 96 (7): 365. Bibcode:1983PhLA...96..365B. doi:10.1016/0375-9601(83)90011-7.
  8. ↑ Lévy, L. P.; Dolan, G.; Dunsmuir, J.; Bouchiat, H. (1990). "Magnetization of mesoscopic copper rings: Evidence for persistent currents". Phys. Rev. Lett. 64 (17): 2074–2077. Bibcode:1990PhRvL..64.2074L. doi:10.1103/PhysRevLett.64.2074. PMID 10041570.
  9. ↑ "Physicists Measure Elusive 'Persistent Current' That Flows Forever". ScienceDaily. October 12, 2009.
  10. ↑ Bluhm, H.; Koshnick, N.; Bert, J.; Huber, M.; Moler, K. (2009). "Persistent Currents in Normal Metal Rings". Phys. Rev. Lett. 102 (13): 136802. arXiv:0810.4384. Bibcode:2009PhRvL.102m6802B. doi:10.1103/PhysRevLett.102.136802. PMID 19392385.
  11. ↑ Birge, Norman O. (2009). "Sensing a Small But Persistent Current". Science 326 (5950): 244–5. Bibcode:2009Sci...326..244B. doi:10.1126/science.1180577. PMID 19815766.
This article is issued from Wikipedia - version of the Tuesday, January 12, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.