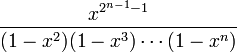Perpetuant
In mathematical invariant theory, a perpetuant is informally an irreducible covariant of a form or infinite degree. More precisely, the dimension of the space of irreducible covariants of given degree and weight for a binary form stabilizes provided the degree of the form is larger than the weight of the covariant, and the elements of this space are called perpetuants. Perpetuants were introduced and named by Sylvester (1882, p.105). MacMahon (1884, 1885, 1894) and Stroh (1888) classified the perpetuants. Elliott (1907) describes the early history of perpetuants and gives an annotated bibliography. There are very few papers after about 1910 discussing perpetuants; (Littlewood 1944) is one of the few exceptions.
MacMahon conjectured and Stroh proved that the dimension of the space of perpetuants of degree n>2 and weight w is the coefficient of xw of
For n=1 there is just one perpetuant, of weight 0, and for n=2 the number is given by the coefficient of xw of x2/(1-x2).
References
- Cayley, Arthur (1884), "A Memoir on Seminvariants", American Journal of Mathematics (The Johns Hopkins University Press) 7 (1): 1–25, doi:10.2307/2369456, ISSN 0002-9327
- Elliott, Edwin Bailey (1895), An introduction to the algebra of quantics, Oxford, Clarendon Press, Reprinted by Chelsea Scientific Books 1964
- Elliott, Edwin Bailey (1907), "On Perpetuants and Contra-Perpetuants", Proc. London Math. Soc. 4 (1): 228–246, doi:10.1112/plms/s2-4.1.228
- Grace, J. H.; Young, Alfred (1903), The algebra of invariants, Cambridge University Press
- Littlewood, D. E. (1944), "Invariant theory, tensors and group characters", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences 239: 305–365, doi:10.1098/rsta.1944.0001, ISSN 0080-4614, MR 0010594
- MacMahon, P. A. (1884), "On Perpetuants", American Journal of Mathematics (The Johns Hopkins University Press) 7 (1): 26–46, doi:10.2307/2369457, ISSN 0002-9327
- MacMahon, P. A. (1885), "A Second Paper on Perpetuants", American Journal of Mathematics (The Johns Hopkins University Press) 7 (3): 259–263, doi:10.2307/2369271, ISSN 0002-9327
- MacMahon, P. A. (1894), "The Perpetuant Invariants of Binary Quantics", Proc. London Math. Soc. 26 (1): 262–284, doi:10.1112/plms/s1-26.1.262
- Stroh, E. (1888), "Ueber eine fundamentale Eigenschaft des Ueberschiebungs-processes und deren Verwerthung in der Theorie der binären Formen", Mathematische Annalen (Springer Berlin / Heidelberg) 33: 61–107, doi:10.1007/bf01444111, ISSN 0025-5831
- Sylvester, James Joseph (1882), "On Subvariants, i.e. Semi-Invariants to Binary Quantics of an Unlimited Order", American Journal of Mathematics (The Johns Hopkins University Press) 5 (1): 79–136, doi:10.2307/2369536, ISSN 0002-9327