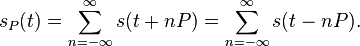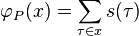Periodic summation

In signal processing, any periodic function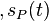, s_P(t)  with period P, can be represented by a summation of an infinite number of instances of an aperiodic function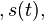, s(t), that are offset by integer multiples of P.  This representation is called periodic summation:

s_P(t) = \sum_{n=-\infty}^\infty s(t + nP) = \sum_{n=-\infty}^\infty s(t - nP).
A Fourier transform and 3 variations caused by periodic sampling (at interval T) and/or periodic summation (at interval P) of the underlying time-domain function.

When 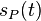 s_P(t)  is alternatively represented as a complex Fourier series, the Fourier coefficients are proportional to the values (or "samples") of the continuous Fourier transform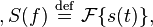, S(f) \ \stackrel{\mathrm{def}}{=} \ \mathcal{F}\{s(t)\},  at intervals of 1/P.[1][2]  That identity is a form of the Poisson summation formula. Similarly, a Fourier series whose coefficients are samples of  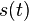s(t)  at constant intervals (T) is equivalent to a periodic summation of  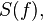S(f),  which is known as a discrete-time Fourier transform.

The periodic summation of a Dirac delta function is the Dirac comb. Likewise, the periodic summation of an integrable function is its convolution with the Dirac comb.

Quotient space as domain

If a periodic function is represented using the quotient space domain 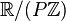\mathbb{R}/(P\mathbb{Z}) then one can write

\varphi_P : \mathbb{R}/(P\mathbb{Z}) \to \mathbb{R}
\varphi_P(x) = \sum_{\tau\in x} s(\tau)

instead. The arguments of 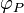\varphi_P are equivalence classes of real numbers that share the same fractional part when divided by P.

Citations

  1. ↑ Pinsky, Mark (2001). Introduction to Fourier Analysis and Wavelets. Brooks/Cole. ISBN 978-0534376604.
  2. ↑ Zygmund, Antoni (1988). Trigonometric series (2nd ed.). Cambridge University Press. ISBN 978-0521358859.

See also

This article is issued from Wikipedia - version of the Monday, August 10, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.