Pentagonal icositetrahedron
| Pentagonal icositetrahedron | |
|---|---|
  Click ccw or cw for spinning versions. | |
| Type | Catalan |
| Conway notation | gC |
| Coxeter diagram |    |
| Face polygon |  irregular pentagon |
| Faces | 24 |
| Edges | 60 |
| Vertices | 38 = 6 + 8 + 24 |
| Face configuration | V3.3.3.3.4 |
| Dihedral angle | 136° 18' 33' |
| Symmetry group | O, ½BC3, [4,3]+, 432 |
| Dual polyhedron | snub cube |
| Properties | convex, face-transitive, chiral |
 Net | |
In geometry, a pentagonal icositetrahedron or pentagonal icosikaitetrahedron[1] is a Catalan solid which is the dual of the snub cube. In crystallography it is also called a gyroid.[2][3]
It has two distinct forms, which are mirror images (or "enantiomorphs") of each other.
Geometry
Denote the tribonacci constant by t, approximately 1.8393. (See snub cube for a geometric explanation of the tribonacci constant.) Then the pentagonal faces have four angles of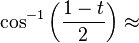 
114.8° and one angle of 
80.75°. The pentagon has three short edges of unit length each, and two long edges of length 
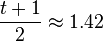. The acute angle is between the two long edges.
If its dual snub cube has unit edge length, its surface area is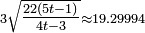 
and its volume is 
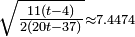.[4]
Orthogonal projections
The pentagonal icositetrahedron has three symmetry positions, two centered on vertices, and one on midedge.
| Projective symmetry |
[3] | [4]+ | [2] |
|---|---|---|---|
| Image |  |
 |
 |
| Dual image |
 |
 |
 |
Related polyhedra and tilings
This polyhedron is topologically related as a part of sequence of polyhedra and tilings of pentagons with face configurations (V3.3.3.3.n). (The sequence progresses into tilings the hyperbolic plane to any n.) These face-transitive figures have (n32) rotational symmetry.
| Symmetry n32 |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | ||||
|---|---|---|---|---|---|---|---|---|
| 232 | 332 | 432 | 532 | 632 | 732 | 832 | ∞32 | |
| Snub figures |
 |
 |
 |
 |
 |
 |
 |
 |
| Config. | 3.3.3.3.2 | 3.3.3.3.3 | 3.3.3.3.4 | 3.3.3.3.5 | 3.3.3.3.6 | 3.3.3.3.7 | 3.3.3.3.8 | 3.3.3.3.∞ |
| Gryro figures |
 |
 |
|
 |
 |
 |
 | |
| Config. | V3.3.3.3.2 | V3.3.3.3.3 | V3.3.3.3.4 | V3.3.3.3.5 | V3.3.3.3.6 | V3.3.3.3.7 | V3.3.3.3.8 | V3.3.3.3.∞ |
The pentagonal icositetrahedron is second in a series of dual snub polyhedra and tilings with face configuration V3.3.4.3.n.
| Symmetry 4n2 |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | ||||
|---|---|---|---|---|---|---|---|---|
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | ∞42 | |
| Snub figures |
 |
|
 |
 |
 |
 |
 |
 |
| Config. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3.∞ |
| Gyro figures |
 |
|
 |
 |
||||
| Config. | V3.3.4.3.2 | V3.3.4.3.3 | V3.3.4.3.4 | V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3.∞ |
The pentagonal icositetrahedron is one of a family of duals to the uniform polyhedra related to the cube and regular octahedron.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
References
- ↑ Conway, Symmetries of things, p.284
- ↑ http://www.metafysica.nl/turing/promorph_crystals.html
- ↑ http://www.tulane.edu/~sanelson/eens211/forms_zones_habit.htm
- ↑ Eric W. Weisstein, Pentagonal icositetrahedron (Catalan solid) at MathWorld
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 730208 (The thirteen semiregular convex polyhedra and their duals, Page 28, Pentagonal icositetrahedron)
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 287, pentagonal icosikaitetrahedron)
External links
- Pentagonal Icositetrahedron – Interactive Polyhedron Model
| ||||||||||||||||||||||||||||||||||||