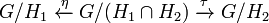Penrose transform

In mathematical physics, the Penrose transform, introduced by Roger Penrose (1967, 1968, 1969), is a complex analogue of the Radon transform that relates massless fields on spacetime to cohomology of sheaves on complex projective space. The projective space in question is the twistor space, a geometrical space naturally associated to the original spacetime, and the twistor transform is also geometrically natural in the sense of integral geometry. The Penrose transform is a major component of classical twistor theory.

Overview

Abstractly, the Penrose transform operates on a double fibration of a space Y, over two spaces X and Z

In the classical Penrose transform, Y is the spin bundle, X is a compactified and complexified form of Minkowski space and Z is the twistor space. More generally examples come from double fibrations of the form

where G is a complex semisimple Lie group and H₁ and H₂ are parabolic subgroups.

The Penrose transform operates in two stages. First, one pulls back the sheaf cohomology groups H^r(Z,F) to the sheaf cohomology H^r(Y,η⁻¹F) on Y; in many cases where the Penrose transform is of interest, this pullback turns out to be an isomorphism. One then pushes the resulting cohomology classes down to X; that is, one investigates the direct image of a cohomology class by means of the Leray spectral sequence. The resulting direct image is then interpreted in terms of differential equations. In the case of the classical Penrose transform, the resulting differential equations are precisely the massless field equations for a given spin.

Example

The classical example is given as follows

• The "twistor space" Z is complex projective 3-space CP³, which is also the Grassmannian Gr₁(C⁴) of lines in 4-dimensional complex space.
• X = Gr₂(C⁴), the Grassmannian of 2-planes in 4-dimensional complex space. This is a compactification of complex Minkowski space.
• Y is the flag manifold whose elements correspond to a line in a plane of C⁴.
• G is the group SL₄(C) and H₁ and H₂ are the parabolic subgroups fixing a line or a plane containing this line.

The maps from Y to X and Z are the natural projections.

Penrose–Ward transform

The Penrose–Ward transform is a non-linear modification of the Penrose transform, introduced by Ward (1977), that (among other things) relates holomorphic vector bundles on 3-dimensional complex projective space CP³ to solutions of the self-dual Yang–Mills equations on S⁴. Atiyah & Ward (1977) used this to describe instantons in terms of algebraic vector bundles on complex projective 3-space. and Atiyah (1979) explained how this could be used to classify instantons on a 4-sphere.

References

• Atiyah, Michael Francis; Ward, R. S. (1977), "Instantons and algebraic geometry", Communications in Mathematical Physics (Springer Berlin / Heidelberg) 55: 117–124, Bibcode:1977CMaPh..55..117A, doi:10.1007/BF01626514, ISSN 0010-3616, MR 0494098 
• Atiyah, Michael Francis (1979), Geometry of Yang-Mills fields, Lezioni Fermiane, Scuola Normale Superiore Pisa, Pisa, ISBN 978-88-7642-303-1, MR 554924 
• Baston, Robert J.; Eastwood, Michael G. (1989), The Penrose transform, Oxford Mathematical Monographs, The Clarendon Press Oxford University Press, ISBN 978-0-19-853565-2, MR 1038279 .
• Eastwood, Michael (1993), "Introduction to Penrose transform", in Eastwood, Michael; Wolf, Joseph; Zierau., Roger, The Penrose transform and analytic cohomology in representation theory (South Hadley, MA, 1992), Contemp. Math. 154, Providence, R.I.: Amer. Math. Soc., pp. 71–75, ISBN 978-0-8218-5176-0, MR 1246377 
• Eastwood, M.G. (2001), "P/p120100", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 
• David, Liana (2001), The Penrose transform and its applications (PDF), University of Edinburgh ; Doctor of Philosophy thesis.
• Penrose, Roger (1967), "Twistor algebra", Journal of Mathematical Physics 8: 345–366, Bibcode:1967JMP.....8..345P, doi:10.1063/1.1705200, ISSN 0022-2488, MR 0216828 
• Penrose, Roger (1968), "Twistor quantisation and curved space-time", International Journal of Theoretical Physics (Springer Netherlands) 1: 61–99, Bibcode:1968IJTP....1...61P, doi:10.1007/BF00668831, ISSN 0020-7748 
• Penrose, Roger (1969), "Solutions of the Zero‐Rest‐Mass Equations", Journal of Mathematical Physics 10 (1): 38–39, Bibcode:1969JMP....10...38P, doi:10.1063/1.1664756, ISSN 0022-2488 
• Penrose, Roger; Rindler, Wolfgang (1986), Spinors and space-time. Vol. 2, Cambridge Monographs on Mathematical Physics, Cambridge University Press, ISBN 978-0-521-25267-6, MR 838301 .
• Ward, R. S. (1977), "On self-dual gauge fields", Physics Letters A 61 (2): 81–82, Bibcode:1977PhLA...61...81W, doi:10.1016/0375-9601(77)90842-8, ISSN 0375-9601, MR 0443823